3.3 Собствени стойности и собствени вектори

3.3.1 Характеристично уравнение

Да се ​​върнем към уравнението (3.21)

Интересен е въпросът дали в пространствотоVnсъществува такъв векторx, който в резултат на трансформация (3.21) преминава във вектораy, който има същата посока като вектораx. Ако отговорът на този въпрос е да, тогава уравнението

къдетое някакъв скалар, който е фактор на пропорционалност. Проблемът за определяне на стойносттаiи съответните векториxi,, удовлетворяващи уравнение (3.25), е известен като проблем със собствените стойности (характерни числа). Векторитеxi, които са решението на уравнение (3.25), се наричат ​​собствени вектори или характеристични вектори, съответстващи на собствени стойностиi.

Векторно-матричното уравнение (3.25) може да бъде пренаписано в следната форма:

къдетоEе съответната матрица на идентичност. Системата от хомогенни уравнения (3.26) има нетривиално решение тогава и само ако детерминантата на матрицата на коефициента е равна на нула:

Разширявайки детерминантата от лявата страна на уравнение (3.27), получаваме полиномn-та степен по отношение на

Уравнение (3.27) или, еквивалентно, уравнение (3.28) е характеристичното уравнение на матрицатаAи неговите корени са собствените стойности (характерни числа) на матрицатаA.

Съгласно теоремата на Виет, коефициентътаnв уравнение (3.28) е равен на произведението на собствените стойности, т.е.

откъдето следва, чеan= (-1)nA. От този израз и от формула (3.29) следва, че произведението на собствените стойности е равно на детерминанта на матрицатаA:

и разширяване на детерминантата E-A ще видим, че коефициентът приn-1има формата-(a11+ a22+…+ann), следователно,сумата от диагоналните елементи на квадратната матрица е равна на сумата от нейните собствени стойности:

(3,31)

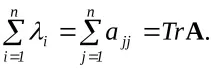
Сумата от диагоналните елементи на матрицата се наричаtraceна матрицата и се обозначава сTrA(първите букви на английската следа са trace).

Чрез въвеждане на нотациятаTk=TrAk, може да се напише полезна формула, свързваща коефициентитеaiна характеристичното уравнение сTkрекурсивна връзка, известна катоформула на Bocher:

---