4.3. кавитационен поток.

P

Нека разгледаме потока течност през тръбата, показана на фиг.11. В мястото на стесняване на потока (участък 2-2) скоростта на течността се увеличава, а налягането намалява и ако стойността му стане равна на налягането на наситените пари, тогава започва интензивно изпаряване (кипене). Движейки се заедно с течността, газовите мехурчета навлизат в разширяващата се част на тръбата, където скоростта намалява и налягането се увеличава. Отделените газове и пари се кондензират и мехурчетата се "свиват".

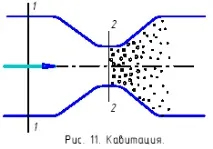
Това явление се нарича кавитация, а потокът е кавитация. Кавитацията е придружена от характерен шум и вибрации, а при продължителна експозиция - постепенно разрушаване (ерозия) на металните стени. Кавитация може да възникне в хидравличните машини, както и на лопатките на витлото.

5. Хидравлични загуби.

5.1. Загуби от триене при ламинарен поток в тръби.

P

в ламинарен поток, диаграмата на разпределението на скороститев напречното сечение на потока е параболична по природа (фиг. 12, а) и се описва от уравнението

, (21)

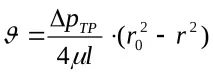
където

е загубата на налягане поради триене в тръба с дължинаl;

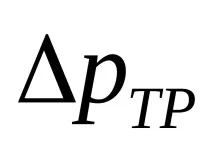
µ- динамичен вискозитет на течността;

rиr0 - текущият радиус и радиусът на тръбата.

Този закон за разпределение на скоростта определя стойността на коефициента на Кариолис за режим на ламинарен поток

= 2 (виж раздел 3.4). В допълнение, зависимостта (21) ви позволява да намерите съотношението на максималните(по оста на потока) и среднитескорости:/= 2.

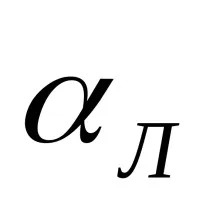
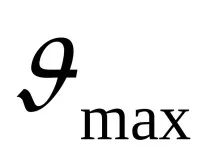
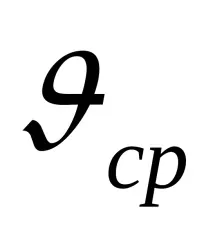
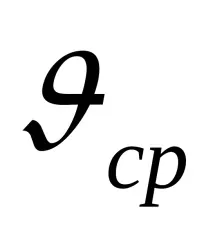
В допълнение, формула (21) позволява да се получи законът за съпротивление за ламинарен режим на поток (закон на Поазей) в кръгла тръба, т.е. зависимост на загубите от дебита Q

(22) или, (23)

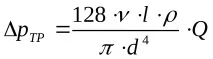
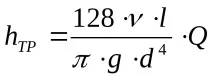
където

и- кинематичен вискозитет и плътност на работния флуид;

-загуба на триене в тръбата.

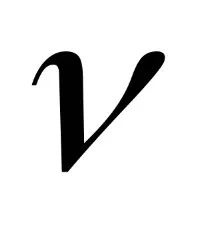
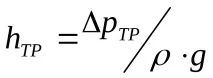
Анализът на зависимостите (22) и (23) ни позволява да заключим, че в режим на ламинарен поток загубите от триене са пропорционални на дебита на течността (фиг. 13).

Формулата за изчисляване на коефициента на Дарси за ламинарен режим може да се получи от съвместното решение на уравнения (22) и (19), първото от които е валидно само за ламинарен поток, а второто за всеки поток. Тогава, като се вземе предвид (20),

. (24)

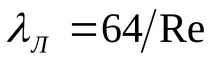
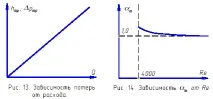
По този начин стойността на коефициента на Дарси в режим на ламинарен поток се определя еднозначно от числото на Рейнолдс.

5.2. Загуби от триене при турбулентно течение в тръби.

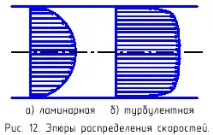
При турбулентен режим на потока, поради интензивно образуване на вихри и смесване на течните слоеве, скоростите

се изравняват по напречното сечение на потока. Следователно диаграмата на разпределението на скоростта има характер на трапец с изгладени върхове (фиг. 12,b), а с увеличаване на скоростите(или числата на РейнолдсRe) тя все повече се доближава до формата на правоъгълник. Коефициентът на Кариолис, отчитащ неравномерното разпределение на скоростите по участъка, - до единица (фиг. 14). Трябва да се отбележи, че при решаване на практически задачи се приема=1.

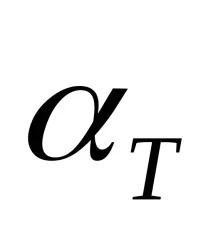
Формулата на Дарси (19) се използва за изчисляване на загубата от триене при турбулентен поток. Но, за разлика от ламинарния режим, коефициентът

зависи не само от числото на Рейнолдс, но и от грапавостта на стените на тръбата. За определяне на този коефициент може да се използва емпиричната формула на Алтшул

, (25)

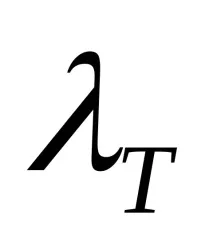
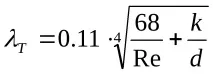
къдетоkе еквивалентната (средна) височина на туберкулите на грапавостта на вътрешните стени на тръбата (избрани от справочника).

В турбулентния режим на течение се разграничават три характерни области на съпротивление.

Първата област е областта на хидравлично гладките тръби, където коефициентът

не зависи от грапавостта, а се определя само от числото на РейнолдсRe. Това се обяснява с факта, че в турбулентен режим в тръбата близо до стената се образува вискозен (ламинарен) слой (поради ниски скорости, виж фиг. 12.6), който скрива неравностите. В областта на хидравлично гладките тръби стойноститеReса относително малки. Следователно във формула (25) първият член68/Reе много по-голям от втория членk/dи последният може да бъде отхвърлен. Тогава от формулата на Алтшул (25) получаваме формулата на Блазиус

. (26)

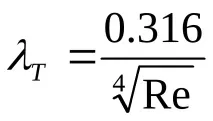
Чрез заместване на формулата на Бласиус (26) във формулата на Дарси (19), като се вземе предвид изразът за числото на Рейнолдс (20), може да се покаже, че в областта на хидравлично гладките тръби загубите от триене са пропорционални на дебита на степен 1,75, т.е.

,

къдетоК- коефициент на пропорционалност.

Във втората област дебелината на вискозния (ламинарен) слой намалява и става съизмерима с височината на грапавите туберкули. Те започват да влияят на съпротивата. Коефициентът

в тази област зависи едновременно от числотоReи от относителната грапавостk/d. Следователно неговата стойност се определя от формулата на Алтшул в общ вид (25). Загубите от триене тук също нарастват с увеличаване на потока, но показателят варира от 1,75 до 2, т.е.

В третата област дебелината на вискозния (ламинарен) слой е изключително малка и неравностите на грапавостта оказват решаващо влияние върху съпротивлението на потока. Това е областта на големите числаRe, следователно във формула (25) първият член68/Reе много по-малък от втория членk/dи стойността68/Reможе да бъде пренебрегната, тогава

, (27)

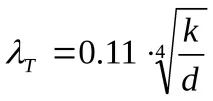
тези. не зависи от брояРейнолдс. Независимостта на

отReопределя пропорционалността на загубите от триене спрямо квадрата на скоростта на потока, т.е.

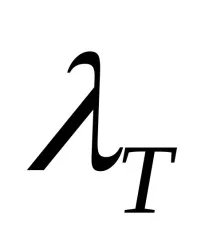
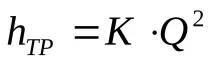
Следователно тази област на съпротивление се нарича зона на квадратично съпротивление.

По-долу е дадена експериментална графика на зависимостта на

отRe, на която коефициентътзависи от съотношениетоke/d, къдетоkeе еквивалентната грапавост, равна на диаметъра на пясъчната фракция, когато се използва изкуствена грапавост, съпротивлението на тръбата е равно до съпротивлението на тръба с естествена грапавост .

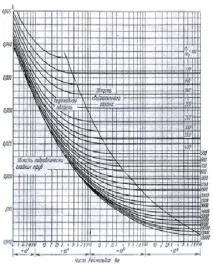
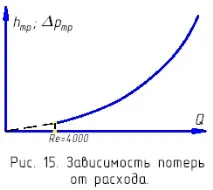
Така, ако при ламинарен режим на течение загубите от триене по дължината са пропорционални на скоростта на потока до първа степен (фиг. 13), то при турбулентен поток тази зависимост е нелинейна. Степента му варира от 1,75 (в областта на хидравлично гладките тръби) до 2 (в областта на квадратичното съпротивление) - фиг. 15.

---