9.1 Построяване на разработки на полиедрични повърхнини
За да се получи разработка на многостенна повърхност, е необходимо да се изреже по някои ръбове и последователно да се комбинират всичките му лица с една равнина, така че да се образува свързана фигура.
За една и съща фигура изгледът на разгънатата повърхност може да бъде различен в зависимост от избраната последователност в подреждането на лицата върху разгънатата.
Всички лица на сканирането са изобразени в пълен размер, така че конструкцията на сканирането се свежда до определяне на естествените стойности на отделните лица на повърхността.
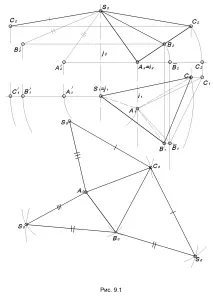
Като пример, разгледайте изграждането на пълно развитие на повърхността на тристенна пирамида SABC (фиг. 9.1).
Първо ще изградим основата на пирамидата, чийто естествен размер A111 ще определим по метода на въртене около проектираната права i. Размерът на страничните ръбове SA, SB и SC може да се определи чрез завъртане около проектираната права линия j. Отсечките S2А2 ' , S2В2 ' и S2С2 ' са равни на дължините на съответните странични ръбове на дадената пирамида.
Изграждането на почистване може да се извърши в следния ред.
На всеки от ръбовете на основата изградете странични лица, като използвате намерените естествени стойности на страничните ръбове S2A2 ', S2B2 ' и S2C2 ' на пирамидата.
Получената плоска фигура е развитие на повърхността на тази пирамида.
Развитието на страничната повърхност на призмата, дадено на фиг. 9.2 ще изпълним по метода на нормален участък.
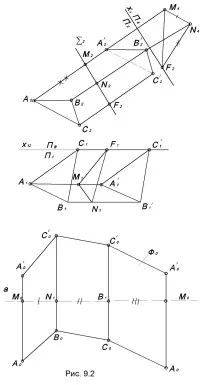
По условие страничните ръбове на призмата са успоредни на равнината P2. Нека пресечем призмата с равнина ∑, перпендикулярна на страничните й ръбове. Сечението на призма от такава равнина се наричанормално. Естествен изглед на нормален разрез M4N4F4 на фиг. 9.2 се намира чрез замяна на равнините P1 с P4.
Познавайки размера на страните на нормалното сечение спрямо дължината на страничните ребра, можете да определите естествения видвсяко лице и изградете мрежа.
Ако разрежем призмата по един от страничните ръбове и разгънем страничната повърхност, тогава страните на нормалното сечение ще бъдат на права линия, перпендикулярна на страничните ръбове.
Процедурата за конструиране на размахване на страничната повърхност на призмата.
Нека дефинираме естествената форма M4N4F4 на нормалното сечение MNF.
През точките M0, N0, F0, M0 начертаваме прави линии, перпендикулярни на правата линия a0, и върху тях начертаваме сегменти, равни на сегментите на страничните ръбове на призмата, като вземем предвид местоположението им спрямо равнината ∑ (отгоре или отдолу). Ф0 - развитие на страничната повърхност на призмата.
Построяване на приблизителни разработки на развойни повърхнини
Теоретично е възможно да се получи точно разгъване на развиващата се повърхност, но на практика това е невъзможно и ненужно. Следователно, когато се конструират повърхностни сканирания, е удобно да се използват графични техники. Криволинейните повърхностисе апроксимират(приблизително се забелязват) от повърхностите на вписани или описани полиедри, чиито лица са триъгълници или четириъгълници; конструиране на разработки на тези полиедри и извършване на заобикаляне на крайните точки на ръбовете на развитата повърхност.
Когато се извършва графично разгъване, винаги е необходимо да се изправят или разгъват кривите линии, принадлежащи на повърхността. За тази цел се използва методътмалки акорди. Както показва името на метода, той се състои в това, че начупена линия се вписва в изправена или неогъваема крива (плоска или пространствена), връзките на която представляват малки хорди на разглежданата крива. Ако кривата трябва да бъде изправена, тогава нейните акорди се нанасят последователно върху някаква права линия и полученият сегмент се приема като приблизителна дължина на дъгата на кривата.
Апроксимиране на дадена разработкаповърхност чрез повърхността на вписан или описан полиедър, в повечето случаи получаваме триъгълни или четириъгълни лица. В случай, че апроксимиращата многогранна повърхност има триъгълни лица, методът на развитие се нарича метод натриангулация.
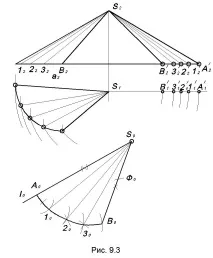
Като пример за прилагане на метода на триангулацията, разгледайте конструкцията на развитие на конична повърхност, дадена от водач a и връх S (фиг. 9.3).
Ние апроксимираме коничната повърхнина с повърхнината на отворена пирамида, вписана в дадената повърхнина. За основа на пирамидата приемаме начупена линия, вписана във водача a. Дължината на сегментите на прекъснатата линия се избира в зависимост от необходимата точност за получаване на размаха: сегментите на прекъснатата линия се избират толкова по-малки, колкото по-високи са изискванията за точност на резултантния размах.
Нека изградим развитие на тази пирамида. Ръбовете на основата му в този случай върху равнината P1 се проектират в пълен размер. За да определим истинските стойности на страничните ръбове на вписан полиедър, използваме метода на въртене. Ако някаква пространствена крива действа като водач или равнината на равнинна крива заема обща позиция, тогава е необходимо също така допълнително да се определят естествените стойности на сегментите, които съставляват прекъснатата линия, вписана в ръководството.
Процедурата за конструиране на приблизително развитие на конична повърхност:
На произволна права l от нейната произволна точка, взета като S, отделяме отсечката A0S0, / A0S0 / = /A2 ’ S2 /.
Построяваме последователно триъгълници 10S020, 20S030 и т.н. върху разработката, съответно съвпадащи с лицата на апроксимиращия многостен.
Заменяме начупената линия A010 2030 B0 с крива, минаваща през върховете на начупената линия. Получени на фиг. 9.3 цифрата Ф0 е приблизителнаразвитие на дадена конична повърхност.
При конструиране на приблизителна разработка на цилиндрична повърхнина, повърхността на призма се използва като приближаваща. Помислете за конструкцията на приблизително развитие на цилиндрична повърхност, като използвате метода на нормалното сечение.
На фиг. 9.4 показва пример за изграждане на цилиндрична повърхност.
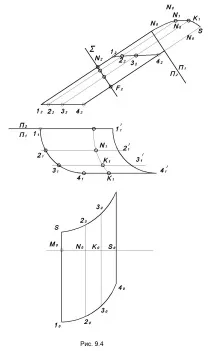
Първо, в дадена повърхност трябва да се впише призма, чиито странични ръбове съвпадат с някои образуващи на цилиндричната повърхност. По-нататъшната конструкция на размаха е подобна на конструкцията на размаха на призмата (виж фиг. 9.2).
Редът за изграждане на почистване е следният:
Разрязваме цилиндъра с равнина ∑, перпендикулярна на образуващите.
Определяме естествената форма на нормално сечение, като заменим равнината П1 с П4 ║∑.
Нека изправим кривата на нормалното сечение, като последователно отделяме дължините на хордите на нормалното сечение /M2N2/ = /M4N4/, /N2K2/ = /N4K4/, /K2F2/ = /K4F4/ на произволна права a2.
През точките M2 N2 K2 F2 начертаваме прави линии, перпендикулярни на a2, отделяме върху тях сегменти, равни на сегментите на съответните генератори (ръбове на призмата) и извършваме байпаси на крайните точки на генераторите.
Получената плоска фигура е приблизително развитие на разглеждания цилиндър.
Трябва да се отбележи, че ако генераторите на цилиндрична повърхност не са успоредни на равнината на проекцията, тогава е препоръчително да се трансформира сложният чертеж, така че генераторите на тази повърхност да заемат позицията на директно ниво.
Изграждане на условни застройки на неразвиваеми повърхнини
В технологията човек често се сблъсква с проблема с конструирането на разгънати повърхности, които не могат да бъдат разкрити. Пример са повърхностите на големисферични резервоари от листова стомана, покрив, отделни тънкостенни корпуси. Теоретично неразвиващите се повърхности не могат да имат развитие. Въпреки това, на практика е необходимо да се прибягва до изграждането на така наречените разработки на тези повърхности, които обикновено се наричат условни.
За да се конструират условни завъртания, дадена повърхност се заменя приблизително (апроксимира) с определен набор от развиващи се повърхности, чиито развития се приемат като условно сканиране на дадена неразвиваща се повърхност. Условното разгъване на неразвиваща се повърхност е коренно различно от приблизителното разгъване на развиваща се повърхност. При конструирането на приблизителен размах, той може да бъде доближен до дадена повърхност с почти всякаква степен на точност чрез увеличаване на броя на лицата на заместващия полиедър. За условно почистване това не може да стане по принцип, т.к колкото и да увеличаваме степента на приближение, в крайна сметка ще имаме не развитие на изследваната повърхност, а развитие на заместващи повърхности.
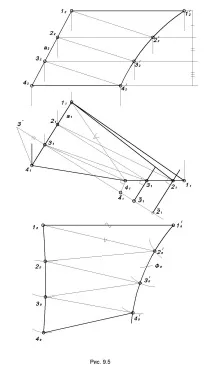
Методът на триангулацията се използва за конструиране на условни завъртания на неразвиващи се повърхности. Помислете, като използвате пример, как е конструирано условното разгръщане на коноида Ф (а, b, П1) (фиг. 9.5).
С помощта на генератори разделяме дадената повърхност на части. Всеки от построените т.н. върху повърхността на неплоските четириъгълници, заместваме го с чифт плоски триъгълници, например: 11 ’ 2 ’ , 12 ’ 2, 22 ’ 3 ’ , 23 ’ 3 и т.н.
Ние изграждаме условното развитие на коноида като развитие на вписана многостенна повърхност, чиито лица са триъгълници 11 ’ 2 ’ , 12 ’ 2, 22 ’ 3 ’ , 23 ’ 3, 33 ’ 4 ’ , 34 ’ 4. Страните на тези триъгълници са 11 ’ , 22 ’ , 33 ’ , 4 4' на хоризонталната равнина се проектират вестествен размер. Естествените стойности на останалите страни на триъгълниците могат да се определят с помощта на метода на правоъгълния триъгълник.
От три страни изграждаме първия триъгълник 1010 ’ 20 ’, към който последователно прикрепяме останалите. Свързвайки върховете на граничните начупени линии с плавни криви, получаваме условна разгъвка на коноида Ф0.
Повърхностите на революция с обща форма принадлежат към класа на неразвиващите се. Следователно за такива повърхности се изграждат условни разчиствания. Методът за получаване на тези разчиствания е както следва. Разглежданата повърхност е приблизително заменена с няколко шлема от развиващи се линейчати повърхности, вписани в дадената повърхност или описани близо до нея. Линейчатите повърхности от своя страна се апроксимират от полиедрични повърхности. Наборът от разгъвки на тези полиедрични повърхности условно се приема като разгъвка на неразвиваща се повърхност на въртене.
Условното разгъване на повърхността на въртене може да се получи по метода на спомагателните цилиндри. Както подсказва името, този метод се състои в замяна на повърхността на въртене с друга повърхност, състояща се от участъци от цилиндрични повърхности.
Например, нека изградим размах на сферата по метода на спомагателните цилиндри (фиг. 9.6). Изграждаме в следния ред:
Нека разделим дадената повърхност на въртене по меридиани на определен брой равни части - дялове. Колкото повече акции, толкова по-висока е степента на приближение.
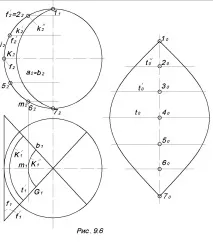
Нека заменим всеки лоб с участък от описаната цилиндрична повърхност, в който водачът е средният полумеридиан на лоба, а образуващите са перпендикулярни на водача.
Цилиндричната повърхност се допира до дадената повърхност на въртене в точките на средния полумеридиан на лоба. Граници за парцел от цилиндричниповърхност са линиите на пресичане на равнините на меридианите, ограничаващи разглеждания дял, със съответната цилиндрична повърхност.
Препоръчително е да разгънете всеки участък от цилиндричната повърхност, като използвате метода на нормалното сечение, като замените цилиндричната повърхност с повърхност на призма.
Помислете за последователността на конструиране на условен размах на четвъртата част на сферата, например участъка между меридианите a и b. За да може условното размахване на сферата да се извърши с голямо приближение до самата сфера, сферата трябва да бъде разделена на 12 части. Но в този случай е направено грубо приближение, за да се направят всички конструкции визуални. Средният меридиан m на дяла (нормалното сечение на апроксимиращата цилиндрична повърхност) се изправя по метода на малките хорди.
Участъци от паралели k, k ’ , k ” и т.н. заменете с отсечки от допирателни t, t ’ , t ” и т.н., които са генератори на цилиндрична повърхност. Сегментите на генераторите се проектират без изкривяване върху P1.
Меридианът m на размаха се изправя в сегмента 1070. През точките 2030405060 начертаваме прави линии, перпендикулярни на 1070, които съответстват на генераторите на цилиндъра.
На нивото на точка 20 ширината на размаха е равна на сегмента t1 ” , на нивото на точка 30 - t1 ’ и т.н. Свързваме краищата на тези сегменти с гладки криви и получаваме условен размах на една част от повърхността на въртене. Копирайки получената цифра по броя на акциите, получаваме пълно условно почистване на сферата. По същия начин можете да разгънете всяка повърхност на революция.
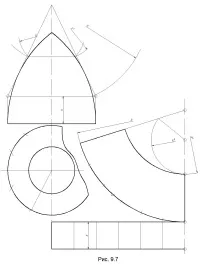
Условното разгръщане на повърхността на въртене може да се изгради и чрез метода на спомагателните конуси. На фиг. 9.7, повърхността на въртене е апроксимирана от отделения от две конични повърхности и една цилиндрична и са конструирани сканирания на тези три отделения. Поради факта, че разглежданитеТъй като повърхността е симетрична, едната й половина може да се разгъне.
Концепцията за процеса на формиране на аксонометрична проекция е дадена в раздел 1.3. Нека разгледаме по-подробно някои свойства на аксонометричните проекции и методите за конструиране на най-често срещаните видове аксонометрични проекции на практика.