формален неврон
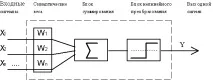
Фиг.4.1. Функционална диаграма на формален неврон от McCulloch и Peets.
Като модел на такъв логически елемент, който по-късно беше наречен "формален неврон", схемата, показана на фиг. 4.1. От съвременна гледна точка формалният неврон е математически модел на прост процесор, който има няколко входа и един изход. Векторът на входните сигнали (идващи през "дендридите") се преобразуват от неврона в изходен сигнал (разпространяващ се по протежение на "аксона") с помощта на три функционални блока: локална памет, блок за сумиране и блок за нелинейна трансформация.
Векторът на локалната памет съдържа информация за теглата, с които входните сигнали ще бъдат интерпретирани от неврона. Тези променливи тегла са аналогични на чувствителността на пластичните синаптични контакти. С избора на тегла се постига една или друга интегрална функция на неврона.
В блока за сумиране общият входен сигнал (обикновено обозначен със символаnet) се натрупва, равен на претеглената сума на входовете:
В модела на McCulloch и Pitts няма времеви закъснения на входните сигнали, така че стойносттаnetопределя общото външно възбуждане, възприемано от неврона. Отговорът на неврона се описва допълнително по начин „всичко или нищо“, т.е. променливата е подложена на нелинейна прагова трансформация, при която изходът (състоянието на активиране на неврона) Y е зададен на единица, ако net>, и Y=0 в противен случай. Праговата стойност (често зададена на нула) също се съхранява в локалната памет.
Трябва да се отбележи, че днес, 50 години след работата на McCulloch и Pitts, изчерпателна теория за синтеза на логически невронни мрежи с произволна функция,очевидно не. Най-напреднали са изследванията в областта на многослойните системи и мрежи със симетрични връзки. Повечето от моделите се основават на различни модификации на формалния неврон. Важно развитие на формалната невронна теория е преходът към аналогови (непрекъснати) сигнали, както и към различни видове нелинейни преходни функции. Нека опишем най-широко използваните типове преходни функции Y=f(net).
Прагова функция (разгледана от McCulloch и Pitts):
Линейна функция, както и нейният вариант - линейна функция с анулиране на отрицателни сигнали:
Както отбелязва S. Grossberg, сигмоидната функция има селективна чувствителност към сигнали с различна интензивност, което съответства на биологичните данни. Най-голямата чувствителност се наблюдава близо до прага, където малки промени в сигналаnetводят до забележими промени в изхода. Напротив, сигмоидната функция не е чувствителна към вариации на сигнала в области значително над или под праговото ниво, тъй като нейната производна клони към нула за големи и малки аргументи.
Наскоро бяха разгледани и математически модели на формални неврони, които отчитат нелинейните корелации между входовете. За невроните на McCulloch и Pitts се предлагат електротехнически аналози, които позволяват директна хардуерна симулация.