KNOW INTUIT, Лекция, 3D графика
Целта на лекцията: Да се усвои теоретичната база, необходима за разбиране на функционирането на механизмите за визуализация на триизмерна графика в XNA
22.1. Координатна система
При работа с триизмерна графика се използват няколко вида координатни системи. За показване на двуизмерни обекти ни беше необходима подходяща координатна система с две оси - хоризонтална ос X и вертикална ос Y. Спомнете си, че координатната система на екрана за двуизмерна графика има начало (точка 0,0) в горния ляв ъгъл на монитора, положителната част на оста X е разположена вдясно от началото, положителната част на оста Y е отдолу.
За да работим с триизмерни обекти, се нуждаем от още една ос - тя се нарича ос Z. Има няколко опции за триизмерни координатни системи, по-специално така наречените дясна и лява система са често срещани. Ще използваме дясната система - тя се използва в XNA Framework. Схематичното му представяне е показано на фиг. 22.1.
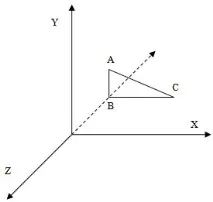
Особеността на тази координатна система е, че началото може да бъде нанесено в долния ляв ъгъл на монитора, положителната част на оста X е вдясно от началото, положителната част на оста Y е отгоре, а положителната част на оста Z е отпред. А това означава, че видимата част на оста Z е нейната отрицателна част. Тази част от оста е така да се каже "в дълбочината на монитора", докато положителната част е "пред монитора". На фиг. 22.1 пунктираната линия показва отрицателната част на оста Z.
В двуизмерна координатна система има концепция за точка - нейните координати са дадени от две стойности - X и Y. Точките съществуват и в триизмерна координатна система - те вече са зададени от три стойности - X, Y, Z.
Точките се използват заза задаване на координатите на върховете на многоъгълници (многоъгълници), по-специално - триъгълници. Така триъгълникът, показан на фиг. 22.1 е даден от три точки - A, B, C.
По правило по-сложните триизмерни обекти се изграждат от триъгълници.
В 3D графиката има такова нещо като лице. Това е плосък обект, който определя множество върхове. В нашия случай обикновеният триъгълник е просто лице. От няколко плоски лица можете да сглобите триизмерен обект.
Колкото повече триъгълници са използвани при изграждането на модела, толкова по-детайлен е той. Точките, съответстващи на върховете на триъгълник, които могат да бъдат начертани в триизмерното пространство, се наричат върхове. Когато работите с 3D графики в XNA, често ще срещнете английския вариант на думата vertex - връх. Може да срещнете множественото число на думата vertex: "vertices" изглежда като "vertices" на английски. Понякога се използва паус от английски за обозначаване на върхове - vertex.
Триъгълникът неслучайно е избран за основна геометрична фигура - първо, този многоъгълник винаги е изпъкнал, и второ, не е възможно да се подредят три точки така, че да не принадлежат на една и съща равнина. Тоест триъгълникът е фигура, която винаги е изпъкнала и плоска, което позволява успешното му използване за 3D графики.
Множеството лица, които образуват 3D обект, се наричат мрежа. Мрежата е набор от триъгълници.
Друга концепция, която ще бъде полезна при работа с триизмерна графика, е концепцията за вектор. Вектор (вектор), подобно на точка, може да бъде дефиниран с три параметъра, но не описва позиция в пространството, апосока и скорост на движение. Векторът има начало и край, за да го дефинирате напълно, трябва да знаете координатите на началната и крайната точка на вектора, т.е. вместо три координатни стойности, имаме нужда от шест стойности. Въпреки това, ако по подразбиране вземем началото на координатите (точка 0,0,0) като начало на вектора, тогава три точки са достатъчни, за да го определим.
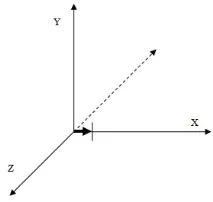
Например вектор с координати (1,0,0) означава: "посока - надясно, скорост - 1". Ако отложим този вектор от началото на координатите, тогава ясно се вижда, че той е насочен точно надясно (фиг. 22.2).
Посоката на вектора се определя от позицията на втората точка спрямо първата (в нашия случай позицията на крайната точка на вектора, която определя вектора спрямо началото), а скоростта се определя от дължината на вектора - тоест разликата между началната и крайната точка. В нашия случай дължината на вектора съвпада с координатите на неговия край.
Има специален вид вектори, наречени нормали. Нормали могат да бъдат построени за лица и за върхове на обект. Нормалните лица са перпендикулярни на тези лица. Те се използват при изчисляване на цвета на даден обект.
22.2. Трансформации в 3D пространството
Познавайки координатите на върховете на многоъгълниците, които съставят обекта, можем да го подредим в пространството. Сега трябва да се справим с промяната на позицията на обектите в пространството. Има няколко основни операции, които могат да се използват за преместване на обекти в 3D пространство. Това са транслация (translation), ротация (rotation) и мащабиране (scale).
Виждаме резултатите от работата на графичната подсистема на триизмерна игра на плосък екран на монитора - триизмерна сцена, симулирана от компютър, се проектира върху двуизмерна повърхност. Когато проектирате, трябва да изберете точка, коятодейства като камера, която ви позволява да виждате триизмерно пространство. От своя страна обектите в триизмерното пространство могат да се движат по определени правила. За управление на всичко това се използват няколко матрици. Това са световната матрица ( World Matrix ), матрицата на изгледа ( View Matrix ) и проекционната матрица ( Projection Matrix ).
Матрицата може да бъде представена като таблица с m реда и n колони. В компютърната графика се използват матрици 4x4. Първите три колони на тази матрица са отговорни за промяна на координатите X, Y, Z на върховете на обекта, участващ в трансформацията.
Световната матрица ви позволява да задавате трансформации - премествания, завъртания и трансформации на обекти.
Матрицата за изглед ви позволява да контролирате камерата.
Прожекционната матрица се използва за регулиране на проекцията на триизмерна сцена на екрана.
Да предположим, че има триъгълник, определен от следните върхове (Таблица 22.1).