Методи за решаване на задачи с параметри.
Намерете всички стойности на параметъраc, за които уравнението
има точно три различни решения.
И ще го решим два пъти: по аналитичния метод, т.е. алгебрични преобразувания и анализ на резултатите от тях и графичен метод. След това ще можете да направите изводи за вашите предпочитания и ще се почувствате по-уверени, когато решавате подобни задачи в USE на ниво профил по математика.
x 2 − 3x + 2 = 0 за x = 1 и за x = 2.
(Уравненията се решават лесно чрез теоремата на Виета, така че не давам пълно решение.)
Тези стойности разделят числовата линия на четири интервала. Във всеки от тези интервали вземаме някакво число, заместваме го в двата израза на подмодула и проверяваме техните знаци. За да не се объркате, по-добре е да направите маркировки директно върху числовата ос.
Така че1) ако x ≤ 0 или x ≥ 2, и двата модула се отварят със знак плюс. Получаваме
Моля, имайте предвид, че границите на пропуските, т.е. Променливите стойности, в които поне един модул е равен на нула, също трябва да "не се губят". Тъй като "+0" и "−0" все още са 0, можете да ги прикрепите както към левия, така и към десния интервал - по ваш избор, но трябва да ги включите само веднъж.
Пристъпваме директно към решението на проблема.
Аналитично решение на задача с параметър.
Преобразуваме всичките три уравнения, получени по-горе, в стандартната форма на квадратно уравнение и ги решаваме.
Дискриминантът на това уравнение е D = (−1) 2 − 4 1 (2 − c) = 4c − 7 ,
следователно за 4c − 7 > 0; c > 7/4; c > 1.75 уравнението ще има два корена:
x1 = 1 − √4c − 7 _____ _________ 2 и x2 = 1 + √4c − 7 _____ _________ 2
За 4c − 7 = 0; с = 7/4; c = 1.75 уравнението ще има един корен x = 1/2, съвпадащ с абсцисата на върхасъответната парабола.
Тези корени обаче ще бъдат корените на оригиналното уравнение с модули само ако принадлежат към интервалите, в които оригиналното уравнение е придобило тази форма, т.е. за x ≤ 0 или x ≥ 2. Спомнете си, че корените на квадратното уравнение са разположени симетрично по отношение на върха на параболата. Абсцисата на върха (x = 1/2) в нашия случай не принадлежи на празнината и се намира между точките x = 0 и x = 2, така че корените на трансформираното уравнение ще бъдат корените на оригиналното уравнение, когато са изпълнени следните неравенства
x1 = 1 − √4c − 7 _____ _________ 2 ≤ 0 и x2 = 1 + √4c − 7 _____ _________ 2 ≥ 2.
Решаваме тези неравенства
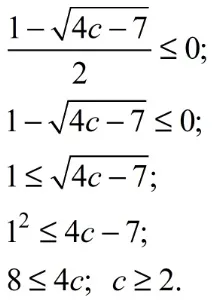
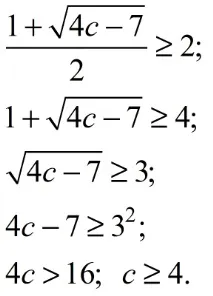
И така, ние обобщаваме: заc ≥ 1.75 корените на уравнението съществуват, но само един от тях може да принадлежи на разглежданите интервали, ако 2 ≤с, и два корена принадлежат на множеството (−∞; 0] U [2; +∞), акос ≥ 4 . Когатоc = 1,75, единственият корен на уравнението не принадлежи към разглежданите интервали на числовата ос.
По подобен начин се занимаваме със следните участъци от числовата ос.
Дискриминант D = 3 2 − 4 1 (c − 2) = 17 − 4c .
При 17 − 4c > 0; c уравнението ще има два корена:
x1 = 3 − √17 − 4c ______ __________ 2 и x2 = 3 + √17 − 4c ______ __________ 2
Корените трябва да принадлежат на интервала(0; 1], но върхът на параболата има абцисаx = 3/2, която е извън този интервал, вдясно от него. Следователно само най-малкият от тях може да бъде корен на първоначалното уравнение с модули при условие 0.
Решаваме съответните неравенства.
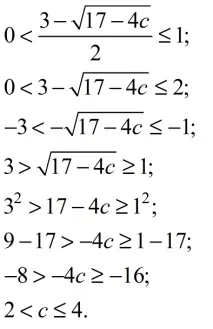
Обърнете внимание, че радикалният знак показва аритметичен корен, който е неотрицателенстойности. Следователно, когато решаваме неравенство, можем да повдигнем на квадрат и двете му части, без да променяме знака на неравенството, само когато и двете имат знак плюс.
Заключение: заc един от тях може да принадлежи към разглеждания интервал, ако е изпълнено условие 2. Когатоc = 4,25, единственият корен на уравнениетоx = 3/2 не принадлежи към интервала на числовата ос (1;2).
Да разгледаме третия интервал (1;2).
Дискриминант D = 9 2 − 4 3 (2 + c) = 57 − 12c .
При 57 − 12c > 0; c уравнението ще има два корена, а при c = 4,75 - единственият коренx = 3/2. В този случай този единствен корен, едновременно - абсцисата на върха на параболата, съвпада със средата на разглеждания интервал. Следователно като условие за принадлежност на два корена към интервала може да се приеме следното - разстоянието между корените не трябва да надвишава дължината на интервала: x2 − x1 √D __ ____ a = √57 − 12c _______ _______ 3
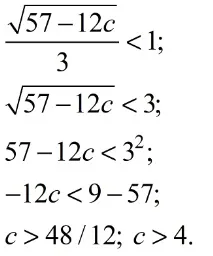
Извод: за 4 ≤c съществуват и принадлежат на разглеждания интервал два различни корена на уравнението. Когатоc = 4,75, уравнението има един коренx = 3/2, който също принадлежи на интервала (1;2).
Нека обобщим. За целта ще използваме и схемата. Нека начертаем числова ос за параметърас. Отбелязваме върху него получените резултати - броя на корените във всяка секция. (Като таблетка: редът показва кой интервал от остаx е дал корени, колоната показва колко корени са получени със съответните стойности на параметъраc.)

Тъй като интервалите не се пресичат (запомнете - граничните точки бяха прикрепени само към един интервал!), корените не могат да се повтарят, т.е. както се изисква от въпроса на проблема, диаграмата показва броя на различните решения. Точно три от тяхще се получи сc = 4 иc = 4.75.
Отговор :s = 4;s = 4,75.
Графично решение на задача с параметър.
За да решите графично уравнение, трябва да начертаете две пресичащи се графики на функции. Една графика на функцията, която съвпада с дясната страна на уравнението, втората - отляво. Въпреки това, графиката на функцията, която съдържа параметъра, ще промени позицията си в зависимост от стойността си. Това означава, че за да се разбере влиянието на параметъра върху резултата от решаването на уравнението, ще е необходимо да се построи тази графика няколко пъти. Следователно е необходимо да се трансформира уравнението, така че частта, която съдържа параметъра, да е възможно най-проста.
В нашия случай, след етапа на разширяване на модула, получихме три уравнения, всяко от които трябва да бъде решено на свой собствен интервал. И в трите, отляво и отдясно, има квадратни тричлени, могат да се построят съответните графики - параболи. Графиката на дясната страна, съдържаща параметъра, ще се движи само по оста Oy, тъй като параметърът присъства само в третия коефициент на тринома. Изглежда, че можете да започнете да изграждате графики. (В края на страницата има примери за чертежи с този подход.) Но нека помислим върху това, не може ли да бъде по-просто? Например, права линия винаги е по-лесна за изграждане от парабола, а хоризонтална линия е още по-лесна за изграждане и анализ. Затова започваме с трансформациите на уравненията, получени в процеса на отваряне на модулите.
И така, от лявата страна на всички уравнения има квадратни триноми, чиито графики са параболи. От дясната страна е постоянна стойност, равна на параметъра. Графиката на функцията y = c е права линия, успоредна на оста x.
Ние изграждаме графики, по-точно на ръка, можете да изграждате само скици на графики, така че няма смисъл да използвате много точки за изграждане на парабола. За да не губите време заненужни изчисления, докато е достатъчно да го изградите върху три точки: не забравяйте да изчислите точно координатите на върха и още две точки, които са лесни за четене устно (например при x = 1 или x = 0). Разглеждайки скиците, ще разберете какво трябва да се изясни по-късно.
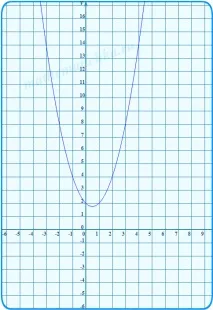
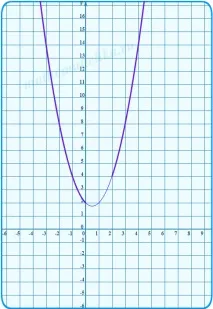
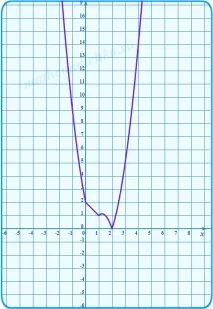
2) Изграждаме парабола y2 = −x 2 + 3x + 2 на същия чертеж, ограждаме тази част от нея, която принадлежи на сечението (0; 1] .
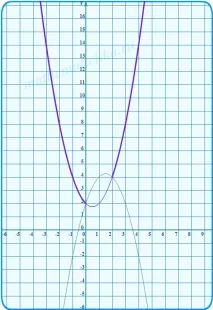
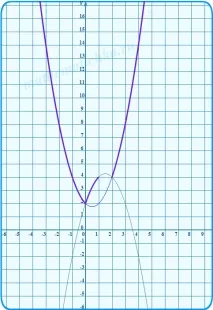
3) Изграждаме парабола y3 = −3x 2 + 9x − 2 на същия чертеж, ограждаме тази част от нея, която принадлежи на сечението (1; 2) .
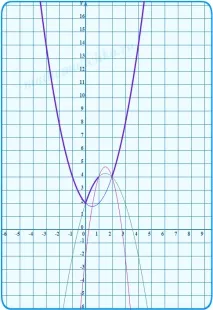
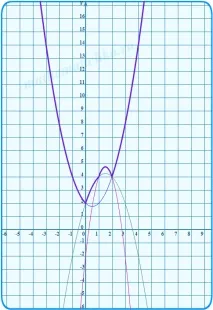
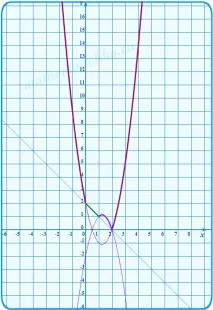
Проверяваме точките на пресичане на параболите една с друга. Очевидно е (според смисъла на модула), че те трябва да се пресичат на границите на интервалите, т.е. би трябвало
Коригираме начертаните на ръка параболи, така че да минават точно през тези точки: (0;2), (1;4), (2;4). И още веднъж оградете цялата графика в нейната цялост.
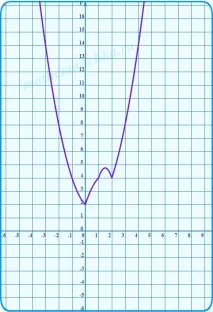
Дясната страна на всички уравнения са прави линии, успоредни на абсцисната ос и пресичащи ординатната ос на ниво y = c. Начертаваме няколко такива линии. Преброяваме броя на пресечните точки с построената графика.
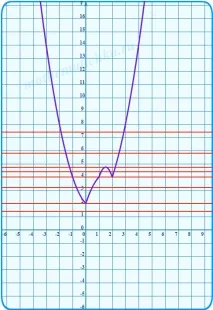
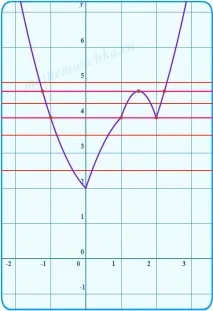
Може да се види "с невъоръжено око", че оригиналното уравнение ще има три пресечни точки и следователно три решения, приc = 4 иc = 4,75.
Важна забележка: Възможно е да се гледа "с невъоръжено око" само ако точките, участващи в отговора, вече са проверени чрез точно изчисление, в противен случай трябва да се провери чрез заместване в уравненията. Нека ви напомня, че по-горе изчислихме върховете на параболите за изграждане, т.е. Ординатата 4,75 вече е потвърдена. Проверихме и точките на пресичане на параболите на границите на интервалите, ордината 4 беше потвърдена от изчислението. Можем да напишем отговор.
Отговор :s = 4;s = 4,75.
Пример за алтернативно графично решение.
Разглеждаме уравненията във вида, в който сме ги получили, като разширим модулите.
1) ако x ≤ 0 или x ≥ 2, 2x 2 − 5x + 2 = x 2 − 4x + c;2) ако 0 − x + 2 = x 2 − 4x + c;3) ако 1 −2x 2 + 5x − 2 = x 2 − 4x + c.
Последователно изграждаме графики на функциите y1 = 2x 2 - 5x + 2, y2 = - x + 2 и y3 = -2x 2 + 5x - 2, като ги ограждаме с дебела линия в желаната област. На същия чертеж изграждаме набор от параболи под формата y = x 2 − 4x + c.
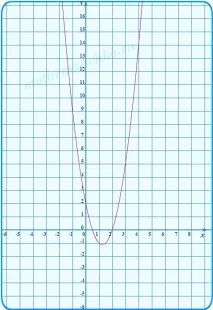
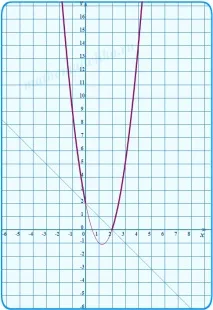
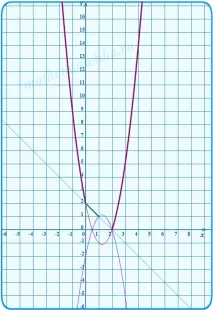
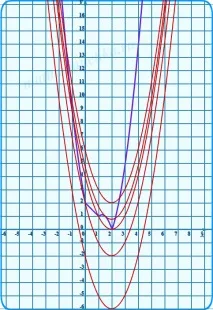
Всичко е точно. Всичко е готово за отговора. Какво можете да видите на тези диаграми? Особено ако са нарисувани и на ръка, като скица? Направете си изводите.
Вижте същозадачи за USE параметрите от минали години :
Задача 18 на един от вариантите на USE през 2015 г.: система от уравнения с параметър. Според мен се решава добре с графичен метод.
Задача 18 на един от вариантите на USE през 2016 г.: уравнение с параметър Според мен тя е добре решена чрез аналитичния метод.
Забележка: Ако откриете грешка или правописна грешка, моля, докладвайте по имейл.

Имате въпроси? желания? коментари? Контакт - [email protected]