Построяване на графика на процес по фазова траектория
Тъй като фазовите траектории не характеризират поведението на изследваната система във времето, може да е необходимо да се изгради процес в системата, за да се завърши оценката на свойствата на системата. Възможно е да се начертае процесът в системата по неговите фазови траектории.
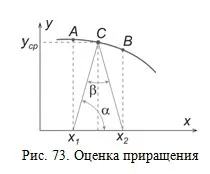
Ако разгледаме малък сегмент AB от фазовата траектория (фиг. 73), тогава поради малката част на сегмента, той може да бъде апроксимиран с прав сегмент. При такова приближение скоростта на изменение на изходната стойност на разглеждания сегмент от фазовата траектория може да се приеме за постоянна и равна на средната скорост yav, съответстваща на средата на сегмента (точка C). Следователно в рамките на интервала
където Δ t е продължителността на процеса на преход на системата от състоянието, съответстващо на точка А от фазовата траектория, към състоянието, съответстващо на точка В.
Ако построите триъгълник x1Cx2, тогава този триъгълник ще бъде равнобедрен, тъй като C е средата на сегмента. От разглеждането на триъгълника следва
Последното уравнение дава съотношението между увеличението на изходната стойност на сегмента AB и продължителността на този процес
Установената връзка между времето на процеса и геометричните характеристики на фазовата траектория ни позволява да начертаем графиката на процеса по фазовата траектория, като използваме следния алгоритъм.
1. Избор на времева стъпка Δ t.
2. Дефиниция на ъгли
3. Построяване на триъгълник от точката x0, съответстващ на началните условия.
4. Повторение на конструкции от точката, получена в резултат на предходната конструкция.
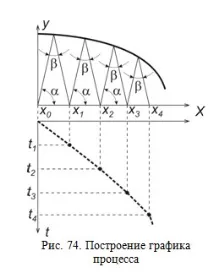
Поради първоначалните предположения, резултатите от построенията дават приблизителна графика на процеса. Грешката на конструиране, на първо място, се определя от избраната времева стъпка Δ t и дължината на сегмента на траекторията, съответстващ на времевата стъпка. Колкото по-малка е избраната стъпка на конструиране, толкова по-висока е точността на конструкцията на преходната графика.