Преобразуване на схема в универсална основа

Схемата, издадена в оригиналната задача, изпълнява функцията ИЛИ-НЕ, следователно ние превеждаме получената факторизирана схема на покритие в универсална база ИЛИ-НЕ.

1. Универсална основа ИЛИ-НЕ.

Обозначението на основния елемент ИЛИ-НЕ е показано на фигура 6.

Фигура 6 - ИЛИ-НЕ основен елемент

Операцията на инверсия се реализира с помощта на елемент ИЛИ-НЕ с един вход (Фигура 7).

Фигура 7 - Изпълнение на операцията NOT (a) с помощта на елемента

Операцията И се получава с помощта на теоремата на де Морган: т.е. чрез подаване на обърнатите стойности на променливите към входовете на елемента ИЛИ-НЕ (Фигура 8)

Фигура 8 - Изпълнение на операция И (а) с помощта на елемента

За извършване на операцията ИЛИ се използват два елемента, тъй като (Фигура 9)

Фигура 9 - Реализация на схемата в универсалната основа ИЛИ-НЕ

Правила за преход от булевия базис И, ИЛИ, НЕ към универсалния базис ИЛИ-НЕ.

1. При преминаване към база ИЛИ-НЕ всички логически елементи се заменят с елементи ИЛИ-НЕ.

2. Независимите входове на елементите И се обръщат, независимите елементи на входовете ИЛИ остават непроменени.

3. На изхода на веригата е инсталиран инвертор, ако изходът е взет от елемента ИЛИ.

В резултат на превода се получава следната схема:

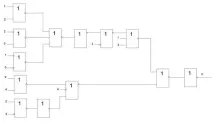
Фигура 10 - Схема в универсалната основа ИЛИ-НЕ

Тъй като двойната инверсия е еквивалентна на липса на операция, веригата може да бъде опростена

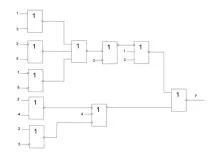
Фигура 11 - опростена схема в универсалната база NOR

Ако изчислим цената на схемата, тогава тя ще бъде:

Ако я сравним с цената на схемата за минимизирано покритие, тогава след извършване на факторизация и прехвърляне на схемата към универсална основа, тогава спестяванията на разходище бъде:

Коефициент на обединяване на входа m=3

Коефициент на обединяване на изхода: n=2

И ако сравним максималните спестявания от оригиналната функция, тогава ще бъде:

---