Превод на цели числа
Резултатът от преобразуването на цяло число винаги е цяло число.
Преобразуване от десетичен в двоичен и шестнадесетичен:
а) първоначалното цяло число се разделя на основата на числовата система, в която се преобразува (на 2 - при преобразуване в двоична бройна система или на 16 - при преобразуване в шестнадесетична); частното и остатъкът се получават;
b) ако полученото частно е по-малко от основата на бройната система, в която се извършва преобразуването, процесът на деление спира, преминете към стъпка c). В противен случай действията, описани в стъпка a), се извършват върху частния;
в) всички получени салда и последното частно се преобразуват в съответствие с таблицата за прехвърляне в цифри на бройната система, в която се извършва преводът;
г) образува се полученото число: неговата най-значима цифра е последното получено частно, всяка следваща най-малка значима цифра се образува от получените остатъци от делението, като се започне от последната и се завърши с първата. Така най-малкият бит от полученото число е първият остатък от делението, а най-значимият е последното частно.
Пример 1 . Преобразувайте числото 19 в двоичната бройна система:
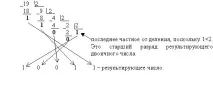
Така 19 = 10011 2 .
Пример 2 . Преобразувайте числото 19 в шестнадесетична бройна система:
Така 19 = 13 16 .
Пример 3. Преобразувайте числото 123 в шестнадесетична бройна система:
Тук остатъкът 11 се преобразува в шестнадесетична цифра B (виж таблицата) и след това тази цифра се включва в числото. Така 123 \u003d 7V 16.
Преобразуване от двоични и шестнадесетични бройни системи в десетични.
В този случай пълната стойност на числото се изчислява по добре познатата формула.
Пример 4. Преобразувайте числото 13 16 в десетичната бройна система. Ние имаме:
13 16 \u003d 1 * 16 1 + 3 * 16 0 \u003d 16 + 3 \u003d 19.
Така че 13 16 = 19.
Пример 5. Преобразувайте числото 10011 2 в десетичната бройна система. Ние имаме:
10011 2 = 1*2 4 + 0*2 3 + 0*2 2 + 1*2 1 + 1*2 0 = 16+0+0+2+1 = 19.
Така че 10011 2 = 19.
Превод от двоичен към шестнадесетичен:
а) оригиналното число е разделено на тетради (т.е. 4 цифри), като се започне от най-малките цифри. Ако броят на цифрите на оригиналното двоично число не е кратен на 4, той се допълва отляво с незначещи нули, докато се достигне кратност 4;
б) всяка тетрада ще бъде заменена със съответната шестнадесетична цифра в съответствие с таблицата.
Пример 6. Преобразувайте числото 10011 2 в шестнадесетична бройна система.
Тъй като броят на цифрите в оригиналното двоично число не е кратен на 4, ние го допълваме отляво с незначещи нули, докато броят на цифрите стане кратен на 4. Ние имаме:
Според таблицата 0011 2 = 11 2 = 3 16 и 0001 2 = 1 2 = 1 16 .
Тогава 10011 2 = 13 16 .
Превод от шестнадесетичен към двоичен:
а) всяка цифра от оригиналното число се заменя с тетрада от двоични цифри в съответствие с таблицата. Ако едно двоично число има по-малко от 4 цифри в таблицата, то се допълва отляво с незначещи нули до тетрада;
б) незначещите нули в полученото число се изхвърлят.
Пример 7. Преобразувайте числото 13 16 в двоична бройна система.
Според таблицата имаме:
- 1 16 = 1 2 и след допълване с незначещи нули на двоичното число 1 2 = 0001 2 ;
- 3 16 = 11 2 и след допълване с незначещи нули на двоичното число 11 2 = 0011 2 .
Тогава 13 16 = 00010011 2 . След като премахнем незначителните нули, имаме 13 16 = 10011 2 .