Псевдоскаларен продукт

продукт

Псевдоскаларен[1] иликосен продуктна вектори a и b>gt; на самолета се нарича номер

a ∧ b = a ⋅ b sin ⁡ θ , =\mathbf \cdot \mathbf\sin \theta ,>

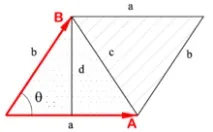
където θ = ∠ ( a , b ) )> - ъгъл на въртене (обратно на часовниковата стрелка) от a до b > . Ако поне един от векторите a и b>gt; нула, тогава поставяме a ∧ b = 0 =0> . Геометрично, псевдоскаларният продукт на векторите е ориентираната площ на успоредника, обхванат от тези вектори. С негова помощ е удобно да се работи с площите на полигоните, да се изразят условията за колинеарност на векторите и да се намерят ъглите между тях.

Псевдоскаларният продукт съществува само за двумерни вектори, неговият аналог в тримерното пространство е тройният скаларен продукт.

  • Линейност: a ∧ ( λ b + μ c ) = λ a ∧ b + μ a ∧ c . +\mu \mathbf )=\lambda \mathbf \wedge \mathbf+\mu \mathbf \wedge \mathbf .> Тук λ , μ са произволни реални числа.
  • Антикомутативност: a ∧ b = − b ∧ a =-\mathbf\wedge \mathbf > .
  • a ∧ b > е псевдоскалар, т.е. инвариант при всички неизродени изометрии, които не включват отражения.
  • Псевдоскаларното произведение a ∧ b > е ориентираната площ на успоредника, обхваната от векторите a и b>gt; .
  • Абсолютната стойност на псевдоскаларното произведение a ∧ b > е площта на успоредника.
  • Ориентираната площ на триъгълник △ A B C се изразява с формулата S ( A , B , C ) = 1 2 ( A B → ∧ A C → ) , >(>\клин >),>
и неговата площ следователно е равна на модула на това количество.
  • Ако разгледаме равнина в триизмерно пространство, тогава a ∧ b = ± ( a × b ) ⋅ n , =\pm (\mathbf \times\mathbf)\cdot \mathbf ,>
    • където “ × ” и “ ⋅ ”, съответно, са векторното и скаларното произведение и n>gt; е единичният вектор на нормалата към равнината. Знакът плюс се взема, ако дясната основа на равнината, допълнена от вектора n > , също формира дясна основа; иначе минус.
    • a ∧ b = 0 =\mathbf > е необходимо и достатъчно условие за колинеарност на ненулевите вектори в равнината. Нулевият вектор обикновено се счита за ортогонален на всеки друг вектор за удобство с по-често срещаното точково произведение, въпреки че това е произволна конвенция.
    • От линейността и антикомутативността следва, че ако ортонормална база ⟨ e 1 , e 2 ⟩ , ∠ ( e 1 , e 2 ) = π 2 , _,\mathbf _\rangle ,

      \ъгъл (\mathbf _,\mathbf _)=>,> и два вектора с координати a = ( a 1 , a 2 ), b = ( b 1 , b 2 ) , , a_),