1 Анализ на оригиналната система
1.1 Функционална схема на затворена система
Функционалната схема на затворена система за управление е показана на фигура 2. Тази верига съдържа в директна верига: усилвателно-преобразуващ елемент (ACE), изпълнителен механизъм (IM), обект на управление (OC) и във веригата за обратна връзка: сензор за обратна връзка (DOS).
Фигура 2 - Функционална схема на затворена система за управление
Функционална диаграма на система за управление със затворен контур за нивото на водата в резервоар е показана на фигура 3. Усилвател на мощност (PA) действа като усилващо-преобразуващ елемент (ECE), DC двигател (DC двигател) действа като изпълнителен елемент, резервоар действа като контролен обект (OC), а потенциометърът действа като сензор за обратна връзка (DOS).
Фигура 3 - Функционална диаграма на затворена система за контрол на нивото на водата в резервоар
1.2 Структурна схема на система за управление със затворен контур
Блоковата схема на затворената система за управление е показана на фигура 4.
Фигура 4 - Структурна схема на затворена система за управление
Трансферните функции на OU, IM и DOS се считат за известни:
Параметри: Ta, Tb, Tc са дадени в техническото задание.
Нека да определим размерите на всички системни параметри:
Приема се, че RPE (PA) е безинерционен, но с ограничена зона на линейност. Статичната характеристика на CPE е показана на фигура 5.
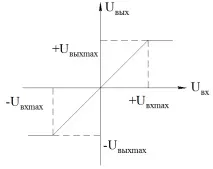
Фигура 5 - Статична характеристика на CPE
Параметри: Uinmax, Uoutmax са посочени в техническото задание.
В началния етап на изследването ще използваме линеаризация на физическо ниво: ще приемем, че усилвателят на мощността има неограничена зона на линейност. Можем да приемем това предположение, тъй като по време на работа на CPE, неговият изходстойността се променя в малък диапазон (±4V) по линеен закон. Блоковата диаграма на линеаризираната система е показана на фигура 6.
Фигура 6 - Структурна диаграма на линеаризирана система
1.3 Анализ на стабилността на оригиналната линеаризирана система чрез алгебричен критерий
Намираме коефициента на усилвателя на мощността от характеристиката, показана на фигура 5 за зона на линейно усилване:
За да се провери линеаризирана система по алгебричен критерий, е необходимо да се запише характеристичното уравнение на затворена система. Това уравнение изглежда така:
(2)
С помощта на софтуерния пакет MathCad трансформираме
характеристично уравнение (Фигура 7):
Фигура 7 - Трансформация XU GS
Крайният изглед на HU ZS:
(3)
Тъй като общият изглед на HU 3S има формата:
(4)
след това записваме коефициентите ХУ ЗС:
Получената система е от 4-ти ред. За проверка на системата по критерия на Хурвиц е необходимо да се провери дали е изпълнено необходимото и достатъчно условие за устойчивост.
Предпоставка: ai>0. Това условие е изпълнено.
Достатъчно условие: всички детерминанти на Hurwitz трябва да са положителни. Тъй като системата е от 4-ти ред, достатъчно е да проверим дали детерминантата от 3-ти ред е положителна. Това следва от факта, че детерминантата от 4-ти ред е равна на произведението на диагоналния минор Δ3 и коефициента a4. Тъй като този коефициент, поради изпълнението на необходимото условие за устойчивост, е положителен, той може да бъде пропуснат при записване на неравенството.
В резултат на това трябва да проверите дали условието е изпълнено:
(5)
След заместване на числовите стойности получаваме:
Достатъчното условие е изпълнено, следователно затворената система е стабилна.