10.3.3. Метод Монте Карло за портфейл от няколко акции
Разгледайте същността на метода Монте Карло за портфейл от две ценни книжа. За портфолио, което включва повече активи, подходът ще остане същият.
Разпределението на стойността на портфейла зависи от степента на корелация на възвръщаемостта на съставните му активи. Най-лесно е да се получи разпределение на стойността на портфейла, когато доходността на акциите варира независимо една от друга или когато има +1 корелация между тях.
Както е отбелязано в параграф 10.3.1, промяната в цената на дадена акция може да се моделира въз основа на уравнение (10.3). Следователно промяната в стойността на акциите в портфейла може да бъде представена чрез равенства:

Удобно е да се извършват изчисления във връзка с портфейл от ценни книжа в матрична форма. Следователно изразите (10.8) и (10.9) ще бъдат представени в матрична форма като:
За простота приемаме в израза (10.10) периодът от време равен на единица. След това ще приеме формата:

Като се има предвид горното, цените на акциите в израз (10.11) могат да бъдат представени като:
Стойността на портфейла в края на първия период може да се намери чрез умножаване на израза (10.12) по вектора на броя на акциите в портфейла:

Формула (10.13) ви позволява да определите стойността на портфейла, когато корелацията на възвръщаемостта на ценните книжа е нула.
Ако корелацията на възвръщаемостта на активите в портфейла е +1 или -1, тогава изразът (10.13) приема формата:
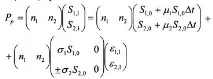
Най-стандартният случай е, когато съотношението на доходността на акциите в портфейла е различно от ± 1. Този факт трябва да се вземе предвид при определяне на стойността му. Резултатите от теста се дават от стойностите на вектора, означени с s. Те трябва да отразяват структурата на корелациите на възвръщаемостта на активите. Необходимото условие може да се моделира с помощта на разлагането на Cholesky. Разлагането на Холецки есиметрична матрица като произведение на долни и горни триъгълни матрици. Следователно корелационната матрица на портфейла (Q) може да бъде представена като:
Знаете ли, че:Можете да спечелите между $20 и $250 в състезаниетоFormula FXна Alpari, като завършите от 1-во до 20-то място. За да участвате, ви е необходима реална сметка, заредена с поне $20. Победителят може да изтегли сумата на наградата по всяко време без никакви ограничения.

Записваме израза (10.14) за портфейл от две ценни книжа:
Произведението на AAT матриците дава резултата:
Нека приравним елементите на корелационната матрица и матрицата на продуктите AAT:
Нека зададем стойностите на вектора? Как:
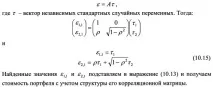
За да се използва разлагането на Cholesky, матрицата A трябва да бъде положително определена. Ако ръководителят включва в модела вариации и корелации, в които се вземат предвид неговите експертни оценки, то не е изключена възможността матрицата да не е положително детерминирана.
Точността на оценката на VaR зависи от броя на извършените тестове. Възможната грешка е обратно пропорционална на корен квадратен от техния брой.
В заключение на този раздел, нека се спрем още веднъж на използването на формула (10.3) за моделиране на пазарната стойност на акция. Формулата включва елемента juSdt. Той определя тренда или скоростта на тренда на движението на цените на акциите. За кратък период от време тенденцията всъщност е неоткриваема и промяната в цената на акциите се дава главно чрез стандартното отклонение. Следователно, ако цената на акциите се моделира за кратък период от време, този термин може да бъде пропуснат. Тогава формула (10.3) приема формата: