1.2 Мерки и единици за представяне, измерване и съхранение на информация
Няма единно научно мнение относно количествения смисъл на понятието "информация". Различните научни направления дават различни определения въз основа на обектите и явленията, които изучават. Някои от тях смятат, че информацията може да бъде изразена количествено, като дават определения за количеството и обема на информацията (мерки за информация), други се ограничават до качествени интерпретации.
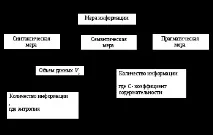
Синтактична мярка за информация
Синтактичната мярка за информация се използва за количествено определяне на безлична информация, която не изразява семантична връзка с обекти.
Количеството данни Vd в едно съобщение се измерва с броя на знаците в него. Обикновено се счита, че броят на двоичните знаци показва количеството данни. Един двоичен знак може да приема само две различни стойности: 1 и 0 (еквивалентно на „да“ и „не“). Двоичен символ се наричаbit(от думите binarydigit - двоична цифра). Преобладаването на двоичната единица за измерване на обема се обяснява с двоичната система за запис на числата, на която се основават съвременните компютри. Традиционно се използва и байт, равен на 8 бита.
Да предположим, че получателят на информацията (наблюдателят) е получил едно и също съобщение два пъти. Той получи двойно количество данни, но получи ли двойно количество информация? Интуицията ни казва, че не - второто копие не съдържа нова информация. Информацията, съдържаща се в съобщението, може да се тълкува от гледна точка на това как е била неизвестна преди това и следователно е нова или неочаквана.
Количеството информация I се определя чрез концепцията за несигурност на състоянието (ентропия). Получаването на информация е придружено от намаляване на несигурността, така че количеството информация може да бъде измереноколичеството несигурност, което е изчезнало.
Нека наблюдателят получи информация за някаква част от реалността (системата) в съобщението. Преди да получи съобщението, получателят е имал някаква предварителна (априорна) информация за системата. Мярката за неговото невежество относно системата е функцията H(), която в същото време служи като мярка за несигурността на състоянието на системата.
След като получи съобщението , получателят придоби информация I() в него, което намали неговото незнание (неопределеността на състоянието на системата), така че тя стана равна на H(). Тогава количеството информация I() за системата, получено в съобщението, ще бъде определено като I() =H() -H() .
По този начин количеството информация в едно съобщение се измерва чрез промяната (намаляването) на несигурността на състоянието на системата след получаване на съобщението.
Ако крайната несигурност H() изчезне, тогава първоначалното непълно знание ще бъде заменено от пълно знание и количеството информация I() =H(). С други думи, ентропията на системата H() може да се разглежда като мярка за информация.
Ентропията на система H() с N възможни състояния, съгласно формулата на Шанън, е равна на
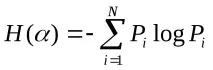
където Pi е вероятността системата да е в i-то състояние.
За случая, когато всички състояния на системата са еднакво вероятни, т.е. техните вероятности са
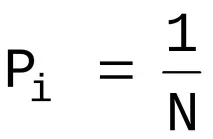
ентропията се определя от отношението
.
Често информацията се кодира с цифрови кодове в една или друга бройна система. Еднакъв брой цифри (символи) в различни бройни системи могат да предават различен брой състояния на показвания обект, което може да се представи като отношение
където N е броят на възможните показани състояния;
m е основата на бройната система (разнообразие от символи, използвани в азбуката);
n е броят знаци всъобщение.
Да вземем пример. Съобщение от n знака се предава по комуникационния канал, като се използват m различни знака. Тъй като броят на възможните кодови комбинации ще бъде N=m n , тогава с еднаква вероятност за възникване на всяка от тях, количеството информация, придобита от абоната в резултат на получаване на съобщение, ще бъде равно на