13. Линейни модели с две повърхнини.

λ1>1

1. Ако λ=2, тогава λφ= 8 4 8 е по-хладна карта

2. Ако λ=0,5, тогава λφ= 2 1 2 е по-плоска карта

В първия случай разликата между покрива на свода и крилата е 4, а във втория 1.

Използвайки различни коефициенти λ, т.е. правейки картата по-плоска или по-стръмна, постигаме сходство с новата карта.

D1 е същото, само че с производни, т.е. интересуваме се от ъглите на падане.

D2 е същото, само че с втори производни, т.е. повърхностна кривина.

Нека разгледаме f= λφ+c, ако приемем f΄= (λφ+c)΄- c изчезва и повърхността може да се измести надолу с някаква константа. Ако вземем f΄΄= (φ+c0+с1х), c0+с1х – обръщаме към нула.

13. Линейни модели с две повърхнини.

Намерена е някаква линейна комбинация от две повърхности φ0 и φ1.

φ0 и φ1 са две сеизмични карти за два различни рефлектора.

Линейни трансформации – една крива се пренася плавно в друга (линейна хомотопия). Разстоянията между кривите се разделят на равни сегменти, след което се свързват.

В областта на модела получаваме:

Ако λ=0, получаваме φ0.

λ е междинна стойност между λ=0 и λ=1, получаваме междинни криви.

Например, карта на плътността на маслото: плътността на маслото намалява към границата на вклиняване, нараства към OWC, за да вземем това предвид, използваме линейна хомотопия.

14. Избор на стабилизиращ функционал.

Повърхнините, които са решение на диференциалното уравнение на Лаплас, имат свойството на минимум на интегралите на квадрата на първата производна. Повърхнините, които са решение на бихармоничното уравнение, имат свойството на минимум от интегралите на квадрата на втората производна.

Минимална кривина - минимум от квадрата на секундатапроизводна.

Понякога е необходимо да се изберат няколко стабилизиращи функционала.

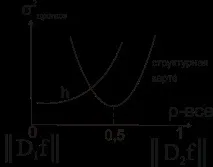
σ 2 прогноза - отклонение от прогнозата.

Най-добрата структурна карта се получава при ρ=0,5, т.е. Взети са 2 стабилизатора. Най-добрата карта на мощността със стабилизатор ║D1f║.

15. Диференциално уравнение и стабилизиращи функционали.

Df=0 - някаква производна на функцията е равна на нула (това е диференциално уравнение)

║Df║ 2 L2 е стабилизиращ функционал.

Повърхностите, които отговарят на диференциалното уравнение на Лаплас, имат свойство на минималната повърхност (т.е. минимумът от интегралите на квадрата на първата производна)

Повърхнините, които са решение на бихармоничното уравнение, имат свойството минимум на интегралите на квадратите на втората производна.

∂ 2 f/∂x 2 +∂ 2 f/∂y 2 =0 – можем да използваме уравнението на Лаплас като стабилизатор.

∂ 4 f/∂x 4 +2∂ 4 f/∂x 2 ∂y 2 +∂ 4 f/∂y 4 =0 – бихармоничното уравнение не може да се използва директно като стабилизатор. Като стабилизатор може да се използва диференциално уравнение от 2-ри ред.

Калкулатор

Услуга за безплатна оценка на цената на работата

1. Попълнете заявление. Експертите ще изчислят цената на вашата работа
2. Изчисляването на цената ще дойде по пощата и SMS

Номерът на вашето приложение

Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.

---