2. Кодиране и измерване на информация.
Има няколко гледни точки относно това какво се счита за информация. Една гледна точка, която изглежда се поддържа от повечето специалисти и неспециалисти, е, че има, така да се каже, два вида информация:
1) техническа информация, която се предава по телеграфни линии и се показва на радарни екрани. Количеството такава информация може да бъде точно изчислено и процесите, които се случват с такава информация, се подчиняват на физически закони.
2) семантична информация, тоест семантична. Това е същата информация, която се съдържа например в литературно произведение. За такава информация се предлагат различни количествени оценки и дори се изграждат математически теории. Но общото мнение по-скоро се свежда до факта, че оценките тук са много условни и приблизителни и все още не можете да проверите хармонията с алгебрата.
Вторият възглед е, че информацията е физическа величина, същата като например енергията или скоростта. По определен начин и при определени условия информацията еднакво описва както процесите, протичащи в естествените физически системи, така и процесите в изкуствено създадените системи.
Както винаги, при наличието на две рязко противоположни мнения, има трето, помиряващо. Привържениците на третия подход смятат, че информацията е една и съща, но количествените оценки трябва да са различни.
Отделно е необходимо да се измери количеството информация, а количеството информация е строга оценка, спрямо която може да се разработи единна строга теория. Освен количеството информация трябва да се измерва и стойността. Но същото нещо се случва със стойността на информацията, както и с концепцията за семантична информация. От една страна, изглежда, че може да се изчисли, но от друга страна, всички тези изчислениявалидни само в ограничен брой случаи. И изобщо, кой може точно да изчисли, да речем, стойността на голямо научно откритие или количеството информация, която се съдържа например в текста на романа „Война и мир“, във фреските на Рафаело или в човешкия генетичен код? Науката не дава отговори на тези въпроси и по всяка вероятност скоро няма да даде.
Разбирайки информацията като един от основните стратегически ресурси на обществото, е необходимо да можем да я оценим както от качествена, така и от количествена гледна точка. По този път има големи проблеми поради нематериалния характер на този ресурс и субективността на възприемането на конкретна информация от различни индивиди на човешкото общество.
2.1. Вероятностен подход за измерване на информация.
Доста трудно е да се дефинира понятието „количество информация“. Има два основни подхода за решаване на този проблем. В края на 40-те години на миналия век един от основателите на кибернетиката, американският математик Клод Ченон, предложи вероятностен подход за измерване на количеството информация.
Съобщение, което намалява наполовина несигурността в знанията на човека, носи 1 единица информация за него. За елементарна единица за измерване на количеството информация се приема 1 бит.
Нека някое съобщение съдържа информация, че е настъпило едно от N равновероятни събития. Тогава количеството информация, съдържащо се в това съобщение, е x бита и числото N е свързано с формулата на Хартли
Например съобщение за резултата от хвърлянето на монета (броят на еднакво вероятните резултати е 2) съдържа x=1 бита информация (2 x = 2). Нека в лотарийния барабан има 32 топки. Колко информация съдържа съобщението за първото изтеглено число? Тъй като появата на която и да е от 32-те топки е еднакво вероятно, тогава 2 x = 32 и x = 5 бита. Помислете повечеедин пример. При хвърляне на зар се използва шестстранен зар. Колко бита информация получава всеки играч, когато хвърля зара? Тъй като всяко лице е еднакво вероятно да изпадне, тогава 2 x = 6, откъдето x = log26 2,585 бита.
Нека сега определим дали съобщенията"жена ще напусне първа сградата"и"мъж ще напусне първа сградата"са равновероятни. Невъзможно е да се отговори недвусмислено на този въпрос. Всичко зависи от това за каква сграда говорим. Ако това е например метростанция, тогава вероятността да излезете първи през вратата е еднаква за мъж и жена, а ако е казарма, тогава за мъж тази вероятност е много по-висока, отколкото за жена.
За проблеми от този вид американският учен Клод Шанън предлага през 1948 г. друга формула за определяне на количеството информация, която отчита възможната неравна вероятност на съобщенията в набор.
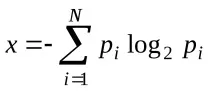
къдетоpiе вероятносттаiтото съобщение да бъде избрано в набора от N съобщения
Лесно се вижда, че ако вероятноститеpiса равни, то всяка от тях е равна на 1/Nи формулата на Шанън се превръща във формулата на Хартли.
Като пример, нека определим количеството информация, свързана с появата на всеки символ в съобщения, написани на български език. Ще приемем, че българската азбука се състои от 33 букви и интервал за разделяне на думите. Според формулата на Хартли x= log234 5,09 бита. В думите обаче различните букви се срещат неравномерно често. Вероятностите за честотата на използване на различни букви се изчисляват на базата на анализ на много големи текстове. Ако това се вземе предвид, тогава според формулата на Шанън получаваме H=4,72. Изчисленията показват, че при равновероятни събития получаваме повече информация, отколкото при неравновероятни.събития.
Когато се изчислява вероятността за настъпване на събитие, често е необходимо да се изчисли броят на различните резултати от експериментите. В този случай се използват различни формули на комбинаториката - раздел на дискретната математика, в който проблемите за избор и подреждане на елементи от определен набор се решават в съответствие с определени правила.
Задача 1.Има 7 пътя, водещи до върха на планината. По колко начина турист може да изкачи планина и да слезе от нея, ако изкачването и слизането се извършват по различни начини?
Задача 2.В групата има 30 души. Необходимо е да се избере ръководител и синдикален представител. По колко начина може да стане това?
Задача 3.Колко трицифрени числа има сразличницифри?
Задача 4. По колко начина могат да се поставят 4 книги на един рафт?
Правило за продукта.Ако първият обект може да бъде избран от някакъв краен набор по k1 начина,
Вторият обект може да бъде избран по k2 начина,
n-тият обект може да бъде избран по kn начини.
тогава произволен набор от изброени n обекта може да бъде избран от този набор по k1 k2 … kn начини.
За да намерите броя на различните пермутации на n елемента, използвайте формулатаPn=n!Например, 6 пермутации могат да бъдат направени от числата 3,5,7: 357, 375, 537, 573, 753, 735.
Задача5. Колко шестцифрени числа, кратни на пет, могат да се съставят от цифрите 1,2,3,4,5,6, при условие че числата не се повтарят в числото?
Задача6. По колко начина могат да се класират 10 отбора в класирането, ако се знае, че няма два отбора с равен брой точки?
Нека има някакво множество, съдържащо n елемента. Всички елементи на такова множество могат да бъдат изброени, т.е.Свържете всеки елемент с едно от естествените числа 1,2,…, n. Такива множества се наричат подредени.
Всякоподреденомножество от k елемента от n-елементно множество се наричаподреждане
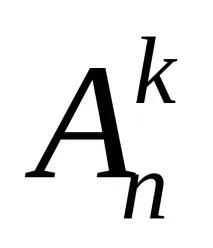
Например нека x=. Тогава един елемент може да образува три подредби: (a), (b), (c); две - шест разположения: (a,b), (b,a), (a,c), (c,a), (b,c), (c,b). За да определите броя
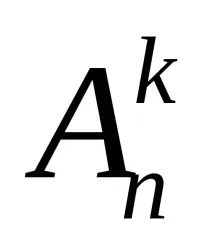
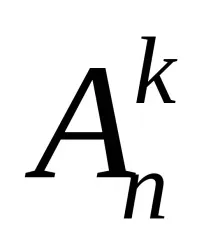
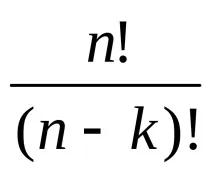
Задача 7. В турнира участват 8 отбора. Колко различни прогнози за разпределението на първите три места могат да бъдат направени?
Задача 8. В семестър се изучават 14 дисциплини. По колко начина можете да планирате часове за понеделник, ако в този ден от седмицата има 5 различни предмета?
Задача10. Назовете всички възможни комбинации от две различни ноти (общо има седем ноти: до, ре, ми, фа, сол, ла, си) Понякога става необходимо да не се вземе предвид редът на елементите, включени в разположението. Например, трябва да съставитеразличнипродукти от числата 3,5,7. Ще има само три такива продукта: 35, 37, 57, тъй като 35=53 и ние не вземаме под внимание реда.
Броят на k-елементните подмножества на n-елементно множество се наричакомбинациии се обозначава с
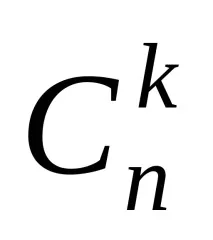
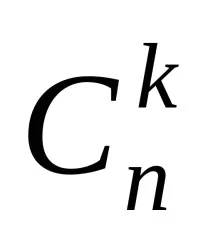
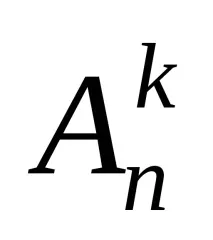
Броят на комбинациите от n елемента по k е
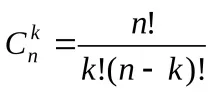
Задача11.Колко изпитни комисии, състоящи се от 7 члена, могат да се съставят от 14 учители?
Задача 12.В турнира са участвали n шахматисти и всеки 2 шахматисти са се срещали веднъж. Колко игри бяха изиграни?
Задача13. Влакът е на един от осемте коловоза. Колко бита информация съдържа съобщението за това къде е влакът?Задача14. Колко бита информация получава играч за цвят, когато произволно се изтегли карта от тестето?
Задача15. Тефтерът лежи на един от двата рафта - горен или долен. Колко бита носят съобщението, че е на долния рафт?
Задача16. Топката е в една от 32 урни. Колко единици информация ще съдържа съобщението за това къде се намира?
Задача17. След изпълнението на едно от еднакво вероятните събития получихме количество информация, равно на 10 бита. Колко възможни събития имаше първоначално?
Задача18. Колко информация ще получи играч 1 след първия ход на играч 2 в игра на тик-так-палеца на поле 4 x 4?