2.2.4 Оценка на значимосттарегресионни параметри
При линейната регресия обикновено се оценява значимостта не само на уравнението като цяло, но и на неговите отделни параметри. За целта за всеки от параметрите се определя неговата стандартна грешка:mbиmа.
Стандартна грешка на регресионния коефициент на параметърbсе изчислява по формулата:
Къде е остатъчната дисперсия за една степен на свобода.
Съотношението на регресионния коефициент към неговата стандартна грешка даваt-статистиката, която се подчинява на статистиката на Student със степени на свобода. Тази статистика се използва за тестване на статистическата значимост на регресионния коефициент и за изчисляване на неговите доверителни интервали.
За да се оцени значимостта на регресионния коефициент, неговата стойност се сравнява със стандартната му грешка, т.е. определяне на действителната стойностt-критерий на Стюдънт:, който след това се сравнява с табличната стойност при определено ниво на значимостαи броя на степените на свобода.
справедливо равенство
Доверителният интервал за регресионния коефициентсе определя като.
Стандартна грешка на параметърасе определя по формулата
Процедурата за оценка на значимостта на този параметър не се различава от тази, разгледана по-горе за регресионния коефициент:t-критерият се изчислява:
Стойността му се сравнява с табличната стойност при степени на свобода.
Значимостта на коефициента на линейна корелациясе проверява въз основа на стойността на грешката на коефициента на корелацияmr:
Действителната стойност наt-теста на Стюдънт се определя като
Тази формула показва, че при двойна линейна регресия , тъй като, както вече беше споменато, . Също така, следователно.
По този начин,тестването на хипотези за значимостта на коефициентите на регресия и корелация е еквивалентно на тестване на хипотезата за значимостта на уравнението на линейната регресия.
Разгледаната формула за оценка на коефициента на корелация се препоръчва да се използва за голям брой наблюдения, а също и акоrне е близо до +1 или –1.
2.3 Интервална прогноза на базата на уравнение на линейна регресия
При прогнозни изчисления, използващи регресионното уравнение, прогнозираната стойностypсе определя като точкова прогнозаxприxp= xk, т.е. чрез заместване на съответната стойностx.в уравнението на линейната регресия,т.е.,и съгласно непрекъснато получаваме интервална оценка на прогнозната стойностy*:
Ако приемем, че прогнозната стойност на фактораxp= xkполучаваме следната формула за изчисляване на стандартната грешка на стойността, прогнозирана по регресионната линия, т.е. тя има израза:
Разгледаната формула на стандартната грешка на прогнозираната средна стойностyза дадена стойностxkхарактеризира грешката в позицията на регресионната права. Стойността на стандартната грешка достига минимум при и се увеличава, когато се „отдалечава“ от всяка посока. С други думи, колкото по-голяма е разликата между u, толкова по-голяма е грешката,, с която средната стойностyе предвидена за дадена стойност. Могат да се очакват най-добри прогнозни резултати, ако факторът на характеристиката x е в центъра на зоната на наблюдение x и не могат да се очакват добри прогнозни резултати, когато се премахне. от. Ако стойността. е извън наблюдаваните стойностиx, използвани при конструирането на линейна регресия, тогава прогнозните резултати се влошаватв зависимост от това как. се отклонява от зоната на наблюдаваните стойности на факторах.
На графиката, показана на фиг. 1, доверителните граници за са хиперболи, разположени от двете страни на регресионната линия. Ориз. Фигура 1 показва как границите се променят с промяна в .: двете хиперболи от двете страни на регресионната линия определят 95% доверителни интервали за средната стойностy, даденаx.
Действителните стойностиyобаче варират около средната стойност.Индивидуалните стойностиyмогат да се отклоняват от размера на случайната грешка ε, дисперсията на която се оценява като остатъчната дисперсия за една степен на свобода. Следователно грешката на предвидената индивидуална стойностyтрябва да включва не само стандартната грешка, но и случайната грешкаs.
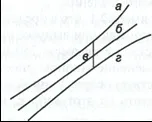
Ориз. 1. Доверителен интервал на регресионната линия:
a -горна доверителна граница;b -регресионна линия;
in —доверителен интервал за at ;
r -долна граница на достоверност.
Средната грешка на предвидената индивидуална стойностyще бъде:
Когато прогнозирате въз основа на регресионното уравнение, трябва да се помни, че стойността на прогнозата зависи не само от стандартната грешка на индивидуалната стойностy,, но и от точността на прогнозата на стойността на фактораx.Стойността му може да бъде зададена въз основа на анализа на други модели въз основа на конкретна ситуация, както и на анализа на динамиката на този фактор.
Разгледаната формула за средната грешка на индивидуалната стойност на атрибутаyможе да се използва и за оценка на значимостта на разликата между прогнозната стойност и някаква хипотетична стойност.