30.1. МРЕЖОВИ МОДЕЛИ. Основни понятия на мрежовия модел
Преди появата на мрежовите методи, планирането на работата, проектите се извършваха в малко количество. Най-известният инструмент за такова планиране беше лентовата диаграма на Гант, чийто недостатък е, че не ви позволява да установявате зависимости между различни дейности.
Съвременното мрежово планиране започва с разбиването на работна програма на дейности. Определят се оценки на продължителността на операциите и се изгражда мрежов модел (графика). Изграждането на мрежов модел ви позволява да анализирате всички операции и да правите подобрения в структурата на модела, преди да бъде внедрен. Изгражда се календарен график, който определя началото и края на всяка операция, както и връзките с други операции по графика. Календарният график идентифицира критични дейности, на които трябва да се обърне специално внимание, за да завърши цялата работа на определената дата. За некритични дейности графикът ви позволява да идентифицирате забавянето на времето, което може да се използва с предимство, когато работата се забави или ефективното използване на трудови и финансови ресурси.
Мрежовият модел е графично представяне на план за изпълнение на комплекс от работи, състоящ се от нишки (работи) и възли (събития), които отразяват логическата връзка на всички операции. Мрежовото моделиране се основава на изображението на планирания комплекс от работи под формата на графика. Графът е диаграма, състояща се от дадени точки (върхове), свързани със система от линии. Сегментите, свързващи върховете, се наричат ребра (дъги) на графа. Насочен граф е този, на който стрелките показват посоките на всички негови ръбове (дъги), което позволява да се определи кой от двата му гранични върха е начален и кой е краен. Изследването на такива мрежи се извършва чрез методите на теорията на графите.
теория на графитеоперира с концепцията за път, който съчетава последователност от взаимосвързани ръбове. Контур означава път, при който началният връх е същият като крайния връх. Мрежовата графика е насочена графа без контури. При мрежовото моделиране има два основни елемента – работа и събитие.
Работата е активен процес, който изисква ресурси или пасивен (изчакване), водещ до постигане на желания резултат.
Фиктивната работа е връзка между резултатите от работата (събития), която не изисква време и ресурси.
Събитието е резултат (междинен или краен) от изпълнението на една или повече предишни дейности.
Път е всяка непрекъсната последователност (верига) от работи и събития.
Критичният път е път, който няма резерви и включва най-интензивната работа на комплекса. Дейностите, разположени на критичния път, се наричат критични дейности. Всички други работи са некритични (ненапрегнати) и имат времеви резерви, които ви позволяват да преместите сроковете за тяхното изпълнение, без да се засяга общата продължителност на целия комплекс от работи.
При изграждането на мрежови модели трябва да се спазват следните правила.
1. Мрежата се показва отляво надясно и всяко събитие с по-висок пореден номер се показва вдясно от предишното. Общата посока на стрелките, изобразяващи задания, обикновено трябва да е отляво надясно, като всяко задание излиза от събитие с по-нисък номер и влиза в събитие с по-висок номер.
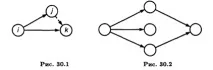
2. Две съседни събития могат да се комбинират само с една работа. За изобразяване на паралелни задачи се въвеждат междинно събитие и фиктивна работа (фиг. 30.1).
3. Мрежата не трябва да има задънени точки, т.е. междинни събития,от която не излиза нито една творба (фиг. 30.2).
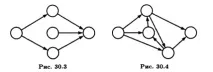
4. В мрежата не трябва да има междинни събития, които не са предшествани от поне една работа (фиг. 30.3).
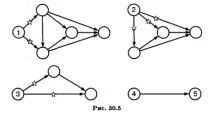
5. В мрежата не трябва да има затворени вериги, състоящи се от взаимосвързани работи, които създават затворена верига (фиг. 30.4). За правилното номериране на събития процедирайте по следния начин: номерирането на събития започва с първоначалното събитие, което получава номер 1. От първоначалното събитие 1 всички изходящи работи се изтриват, в останалата мрежа отново се открива събитие, което не включва никаква работа. На това събитие се дава номер 2. След това заданията, произтичащи от събитие 2, се задраскват и събитието отново се намира в останалата част от мрежата, която не включва никаква работа, присвоява му се номер 3 и така нататък до последното събитие. Пример за номериране на мрежова диаграма е показан на фиг. 30.5.
Продължителността на работата се определя въз основа на действащите стандарти или според експертни оценки на специалисти. В първия случай оценките на времето са детерминистични (еднозначни), във втория случай те са стохастични (вероятностни).
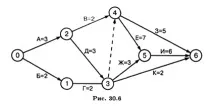
Помислете за пример за програма за създаване на нов домакински уред, който е търсен сред населението. Необходимите данни са дадени в табл. 30.1.
Въз основа на данните в таблицата ще изградим мрежов график за създаване на устройство, като вземем предвид горните препоръки (фиг. 30.6).