3.01.2. Основни видове графики
Графът се наричаПразен, акоE(G) = Æ, т.е. ако няма ребра. Празен граф от редNсе означава с0N. Граф01 се наричаТривиален.Граф, в който всеки два върха са свързани с ребро, се наричаПълен.Пълен граф от редNсе означава сKn.
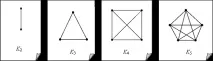 |
Лесно е да се изчисли, че графикатаKnимаN(N-1)/2 ребра.
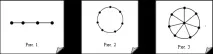
Графика на формата, показана на фиг. 1 се наричаПроста верига.Проста верига от редNсе обозначава сPn(Фигура 1 показва веригаP4). Проста веригаPnИмаN–1 ръба.
Затворени вериги, т.е. графики като на фиг. 2 се наричат Прости цикли.Прост цикъл от порядъкNсе означава сCn(фиг. 2 показва проста схемаС7). Ясно е, че една проста веригаCnима толкова ръбове, колкото има върхове, т.е.N.
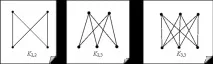
Ако в двустранен граф всеки два върха от различни части са свързани с ребро, тогава такъв граф се наричаПълен двустранен. Пълен двустранен граф сNвърха в една част и сMвърха-- в другия се обозначава сKn,M. Вижте примери:
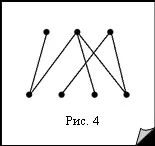
ГрафикитеK1,Nсе наричат звездни графикиилизвезди.
Ясно е, че има графики, които могат едновременно да бъдат приписани на няколко типа. НапримерK3=C3,K2=P2,K2, 2 =C4,K4=W3.