6.2 Директна резекция (формули на Гаус)

Ако при решаването на задачата се окаже, че няма видимост между началните точки, тогава се използватформули на Гаус. За целта съответно в точкитеAиBсе измерват ъглите1и2, а за контрол на правилното определяне на координатите на точкатаPъгълът3 се измервав точкаC(Фигура 17).

Процедурата за решаване на проблема:

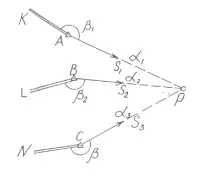
Фигура 17 Директна резекция (формули на Гаус)

За решаване на задачата са необходими два дирекционни ъгъла, третият е за контрол и повишаване на точността.

2. Формулите на Гаус се извеждат от известната връзка

tg1=

(87)

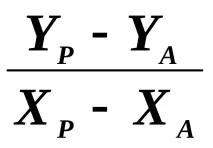
Тези две равенства представляват система от две уравнения с две неизвестни XP и YP. Изваждаме уравнение (89) от уравнение (88), получаваме

XP = (90)

Стойността на ординатата се изчислява в този случай по формулите:

Формулите на Гаус (90) и (91) се използват за директно изчисляване на стойностите на координатите на точкатаР.

3. Изваждаме от двете части на равенството (90)XAи намалявайки дясната страна до общ знаменател, ще имаме

XP– XA=(92)

Така намираме

XP– XB=(93)

Получените две равенства, заедно с равенствата (88) и (89), са формулите на Гаус за нарастване на координатите. След изчисляването им координатите на точкатаРсе определят два пъти:

XP \u003d XA + (XP - XA) \u003d XB + (XP - XB)

4. Използване на координатите на друга двойка точки от данниBиCи съответните им дирекционни ъгли2и3, координатите на точкатаPсе изчисляват за втори път.

Например формулите на Гаус за директно изчисляване на стойностите на координатите на точкатаРза втората двойка

XP=(95)

Стойността на ординатата се изчислява в този случай по формулите:

YP = YВ + (XP - XВ) tg 2 или (96)

5. Оценка на точността. Допустимостта на несъответствието между стойностите на координатите, получени с две решения на проблема, може да се определи по същите формули, както при решаването на проблема с помощта на формулите на Йънг.

6.3 Резекция (формули на Kneissl)

Свързването на ходовете може да се извърши чрез решаване на задачата за намиране на координатите на точкаPс помощта на три началниA,B,C(Фигура 18), разположени на значително разстояние от определяната.

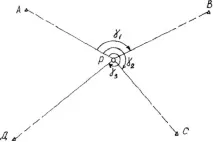
Фигура 18 Резекция

За контрол на измерванията се правят наблюдения в точкаD. По този начин, за да се реши задачата с управление, е необходимо да се видят четири начални точки от определената точкаРи да се измерят три ъгъла в определената точка. Този проблем се решава най-лесно с помощта на формулите на Kneissl.

Процедурата за решаване на проблема:

Следователно можете да напишете:

tg 2 = tg (1 + 1) =

(97)

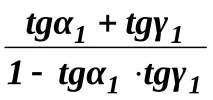
2. За да съкратим записите в по-нататъшния изход, преместваме началото на координатите в точкатаА. Тогава в новата координатна система ще бъде:

3. Известно е, че tg VR =

(98)

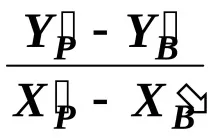
и tg 1 =

. Тогава имаме

(99)

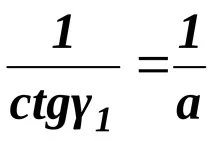
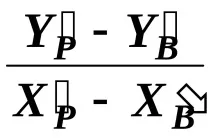
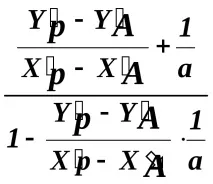
Тъй като ХА = 0 и YA = 0, получаваме

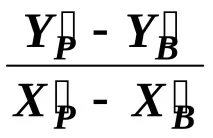
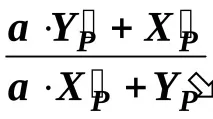
Разширявайки скобите и прегрупирайки термините, имаме

(aYВ - XВ) XP - (aXВ + YВ) YP = -( Х) 2 –( Y) 2

Означавайки коефициентите при Х и Y в първото от двете равенства с K1 и K2, а във второто с K3 и K4, ще имаме система от две уравнения с две неизвестни.

I K1  XP - K2  YP = - Х 2 - Y 2

Като извадим второто уравнение от първото уравнение, получаваме

(К1 – К3)  XP -(К2 – К4)  YP = 0, откъдето следва, че

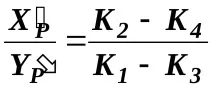
4. Означете

(102)

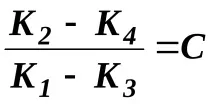
след това

или XP = С  YP (103)

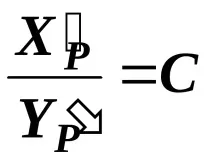
Замествайки този израз в уравнения I и II, получаваме

YP=(104)

7. сtg РД =

; контрол RD - RA = 3 изчислено (106)

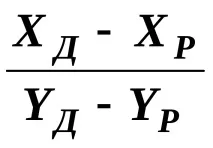
Графична оценка на точността по формулите на G.E. Сомовопределяне на позицията на точкатаP, получена от разтвора на резекцията, се извършва в следната последователност.

ТочкиA,B,C,DиPсе нанасят по известни и получени координати в такъв мащаб, че да няма посоки по-малки от 5 - 6 см>1 ,S2,S3иS4. Градиентите на посоката се изчисляват по формулатаqi=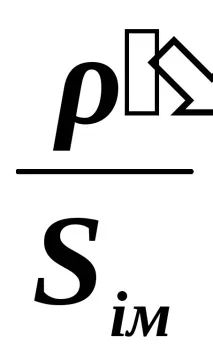

;= 206265. В приетия мащаб градиентите се изчертават от точкатаРв съответните посоки, свързват краищата на градиентите и получават два инверсионни триъгълникаA1B1C1иB1C1D1(Фигура 21). От върховетеA1иC1на първия инверсионен триъгълник са начертани височиниh1иh3от противоположните страни и ги измерете. От върховетеВ1иД1на втория инверсионен триъгълник по подобен начин се намиратh2иh4.

За графична оценка на точността, съгласно формулите на Г. Е. Сомов, се определят средноквадратичните грешки на позицията на точкатаР, получени съответно в първото и второто решение:

M1=

; (107)

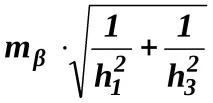
M2=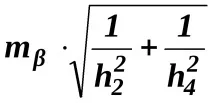

; (108)

M =

; (109)

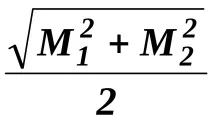
къдетоm- средна квадратична грешка при измерване на ъгъл.

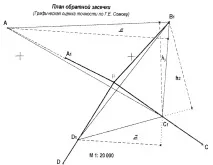
Фигура 19 Графична оценка на точността от G.E. Сомов

1. Необходими изходни данни за определяне на координатите на допълнителна точка по права линия по формулите на Юнг.

2. В каква последователност се решава директен сериф с помощта на формулите на Гаус?

3. Последователността на решаване на резекцията с помощта на формулите на Kneissl.

4. Как се определя графичната оценка на точността по формулите на G.E. Сомов?

5. Напишете формула за определяне на градиентите на посоката.