686. Намерете обема на правилна триъгълна пирамида със страничен ръб l, ако: а) страничният ръб сключва ъгъл φ с равнината на основата; б) страничният ръб сключва ъгъл α със съседната страна на основата; в) плоският ъгъл при върха е равен на β.

Решетник по геометрия за 10 клас (Л. С. Атанасян, 2001), задача№ 686 към глава „Глава VII. Тел томове § 3. Обемът на наклонена призма, пирамида и конус.

686. Намерете обема на правилна триъгълна пирамида със страничен ръб l, ако: а) страничният ръб сключва ъгъл φ с равнината на основата; б) страничният ръб сключва ъгъл α със съседната страна на основата; в) плоският ъгъл при върха е равен на β.

От правоъгълен триъгълник ΔADO:

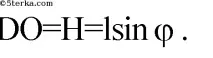
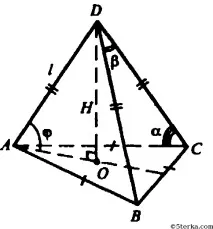
Точка O е центърът ΔABC, OA е радиусът на описаната окръжност около ΔABC.

По закона на синусите:

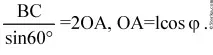
б) ΔADC е равнобедрен.

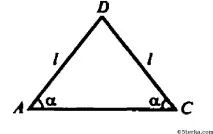
По закона на косинусите имаме:

Нека изчислим дължината на отсечката OA, OA=R, където R е радиусът на окръжността, описана около ΔABC.

в) ΔBDC е равнобедрен. Според закона на косинусите:

В триъгълник ΔABC: OA е радиусът на описаната окръжност:

---