9. Закон за разпределение на случайна величина. Проверка на хипотези за законите на разпределение на случайни величини.
Изложена е нулевата хипотеза H0: неизвестната функция на разпределение F(x) на изследваната случайна променлива X е разпределена според някакъв теоретичен закон, например според нормалния закон:H0:F(x)=Ftheor(х).
Всеки закон може да се разглежда като този теоретичен модел Ftheor(x), например експоненциално или биномиално разпределение. Това се определя от същността на изследваното явление, както и от резултатите от предварителната обработка на наблюденията: формата на графиката на разпределението, връзката между извадковите данни.
Изложена е алтернативна хипотеза, че тази обща съвкупност не е разпределена според закона Ftheor(x):
H1:F(x)Ftheor(x).
Нивото на значимост е зададено, например, α≤0,05.
Ако искаме да проверим дали емпиричните данни са в съответствие с нашето хипотетично предложение по отношение на теоретичната функция на разпределение или не, тогава използваме теста за съответствие.
Тестът за съответствиее критерий за проверка на хипотезата на предложения закон на неизвестното разпределение.
Помислете за един от тях, използващ разпределениетоX2 и наречентест за съответствие на Pearson. Този тест не изисква никакви предположения относно параметрите на популацията, от която е съставена извадката. Това е непараметричен критерий.
Нека приложим критерияХ2 (хи-квадрат), за да проверим нулевата хипотеза H0, че населението е разпределено според нормалния закон.
Критерият предполага, че резултатите от наблюденията са групирани в вариационна серия и разделени на класове.
Въз основа на извадка от обем n, ние конструираме емпирично разпределение Femp(x):
и го сравнете с предполагаемото теоретично разпределение, изчислено при предположениетонормален закон за разпределение.
Като критерий за тестване на нулевата хипотеза ще вземем произволна стойност:
,
където k е броят на класовете.
От таблиците намираме Хcrit 2 (α≤0.05, f=k-3).
Сравнете, ако Xnabl 2 2 (α, f) => H0 - това разпределение се подчинява на нормалния закон.
В противен случай не се подчинява на нормалния закон.
10. Функционални и корелационни зависимости. Линеен корелационен коефициент и неговите свойства.
Функционалната зависимост–е зависимост от формата y=f(x), когато всяка възможна стойност на случайната променлива X съответства на една възможна стойност на случайната променлива Y.
Корелационната зависимост–е статистическа зависимост, която се проявява във факта, че при промяна на една от стойностите се променя средната стойност на другата:
=f(x).
За изследване на корелационната връзка е удобно да се уточнят статистически данни за зависимост под формата на корелационна таблица или под формата на двумерна извадка.
Схемата на експеримента е следната: нека има извадка с размер n от генералната съвкупност N. На всеки обект от извадката се определят числените стойности на характеристиките, между които се изисква да се установи наличието или липсата на връзка. Така получаваме 2 серии от числени стойности.
За яснота на получения материал всяка двойка може да бъде представена като точка в координатната равнина. По абсцисната ос са нанесени стойностите на единия вариационен ред - xi, а по ординатната ос - на другия - yi.
Такова изображение на статистическа връзка се наричакорелационно полеиликорелационно поле от точки.То създава цялостна картина на корелацията.
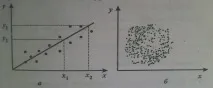
А) точките са групирани по някаква посока, това показва наличието на линейнакорелация между характеристиките.
Б) точките са неравномерно разпределени, това показва, че няма линейна корелация
На практика изследователят често може да се интересува не от самата зависимост на една променлива от друга, а по-специално от характеристиката на близостта на връзката между тях, която може да бъде изразена с едно число. Тази характеристика се наричаизвадков линеен коефициент на корелацияr.
Изискванияза корелационен анализ: корелационният анализ е метод, използван, когато данните могат да се считат за случайни и избрани от популации, разпределени спореднормалниязакон.
Коефициентът на линейна корелация на извадката r характеризира плътността на линейната връзка между количествените характеристики в извадката:
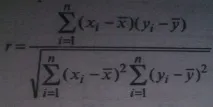
Ако r> 0, тогава корелацията между променливите е пряка, с r 0,9 - много силна
При r=1 - функционална зависимост y=f(x)
Колкото по-близо е r до 0, толкова по-слаба е връзката.
При r=0 няма линейна корелация.
rxy=ryx – симетрични случайни променливи
x и y могат да се разменят, без да се засяга стойността на r.
Ако всички стойности на променливите се увеличат (намалят) с еднакъв брой или с еднакъв брой пъти, тогава стойността на корелационния коефициент няма да се промени
Коефициентът на корелация е безразмерна величина.