Абстрактни повърхности от втори ред
Повърхности от втори редса повърхнини, които са определени в правоъгълна координатна система чрез алгебрични уравнения от втора степен.
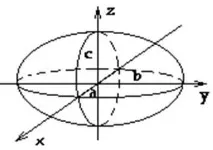
Уравнение (1) се наричаканонично уравнение на елипсоида.
Задайте геометричния изглед на елипсоида. За да направите това, разгледайте сеченията на този елипсоид с равнини, успоредни на равнинатаOxy.Всяка от тези равнини се определя от уравнение от видаz=h, къдетоhе произволно число, а правата, която се получава в сечението, се определя от две уравнения
(2)
Нека проучим уравнения (2) за различни стойностиh.
1) Ако >c(c>0), тогава уравнения (2) дефинират въображаема елипса, т.е. няма точки на пресичане на равнинатаz=hс този елипсоид.
2) Ако , тои правата (2) се изражда в точки (0; 0; +c) и (0; 0; -c) (равнините докосват елипсоида).
3) Ако , тогава уравнения (2) могат да бъдат представени като
откъдето следва, че равнинатаz=hпресича елипсоида по елипса с полуоси и . Тъй като стойностите на и нарастват и достигат максималните си стойности при , т.е. в сечението на елипсоида с координатната равнинаOxyсе получава най-голямата елипса с полуоси и .
Подобна картина се получава, когато дадената повърхност се пресича от равнини, успоредни на координатните равниниOxzиOyz.
По този начин разглежданите сечения позволяват да се изобрази елипсоидът като затворена овална повърхност (фиг. 156). Стойноститеa, b, cсе наричат полуосина елипсоида. Когаa=b=cелипсоидът есферота.
2.Хиперболоид с една лента.
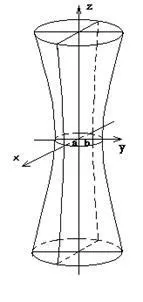
(3)
Уравнение (3) се нарича канонично уравнение на еднолентов хиперболоид.
Задайте типа повърхност (3). За да направите това, разгледайте сечението на неговите координатни равниниOxy(y=0)иOyx (x=0).Получаваме съответно уравненията
И
от което следва, че в сеченията се получават хиперболи.
Сега разгледайте сеченията на този хиперболоид с равнини z=h, успоредни на координатната равнинаOxy.Линията, получена в сечението, се определя от уравненията
или (4)
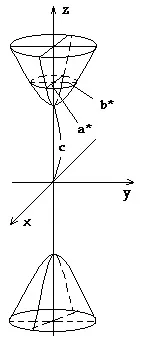
от което следва, че равнината z=h пресича хиперболоида по елипса с полуоси и ,
достигайки най-ниските си стойности при h=0, т.е. в сечението на този хиперболоид координатната ос Oxy произвежда най-малката елипса с полуоси a*=a и b*=b. При безкрайно нарастване величините a* и b* нарастват безкрайно.
По този начин разглежданите сечения позволяват да се изобрази хиперболоид с една лента като безкрайна тръба, безкрайно разширяваща се, докато се отдалечава (от двете страни) от равнината Oxy.
Величините a, b, c се наричат полуоси на еднолентов хиперболоид.
3.Двуслоен хиперболоид.
Двуслоен хиперболоид е повърхност, която в някаква правоъгълна координатна система се определя от уравнението
(5)
Уравнение (5) се нарича канонично уравнение на двуслоен хиперболоид.
Нека установим геометричната форма на повърхността (5). За това помислетенеговите сечения с координатните равнини Oxy и Oyz. Получаваме, съответно, уравненията
И
от което следва, че в сеченията се получават хиперболи.
Сега разгледайте сеченията на дадения хиперболоид с равнини z=h, успоредни на координатната равнина Oxy. Линията, получена в сечението, се определя от уравненията
или (6)
от което следва, че за >c (c>0) равнината z=h пресича хиперболоида по елипса с полуоси и . С увеличаване на стойността, a* и b* също се увеличават.
При уравнения (6) координатите само на две точки удовлетворяват: (0; 0; + c) и (0; 0; - c) (равнините се допират до дадената повърхност).
Когато уравнения (6) определят въображаемата елипса, т.е. няма пресечни точки на равнината z=h с дадения хиперболоид.
Величината a, b и c се наричат полуоси на двулистния хиперболоид.
4.Елиптичен параболоид.
Елиптичен параболоид е повърхност, която в някаква правоъгълна координатна система се определя от уравнението
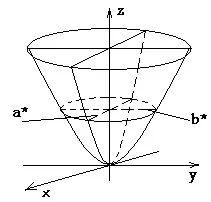
(7)
Уравнение (7) се нарича канонично уравнение на елиптичен параболоид.
Разгледайте сеченията на дадената повърхност с координатните равнини Oxy и Oyz. Получаваме, съответно, уравненията
И
от което следва, че в сеченията се получават параболи, симетрични спрямо оста Oz, с върхове в началото.
Сега разгледайте сеченията на този параболоид с равнини z=h, успоредни на координатната равнина Oxy. Линията, получена в сечението, се определя от уравненията
или (8)
от което следва, че когато равнината z=h пресича елипсовиден параболоид по елипса с полуоси и . С увеличаване на h, a и b също се увеличават; за h=0 елипсата се изражда в точка (равнина z=0се отнася до дадения хиперболоид). За h 0, q> 0.
Уравнение (9) се нарича канонично уравнение на хиперболичен параболоид.
Да разгледаме сечение на параболоид с равнината Oxz (y=0). Получаваме уравнението
(10)
от което следва, че в сечението се получава парабола, насочена нагоре, симетрична спрямо оста Oz, с връх в началото. При разрези на повърхността с равнини, успоредни на равнината Oxz (y=h), се получават и параболи, насочени нагоре.
разгледайте сечение на дадения параболоид с равнината Oyz (x=0).
от което следва, че в този случай в сечението се получава парабола, но вече насочена надолу, симетрична спрямо оста Oz, с връх в началото. Разглеждайки сеченията на параболоида с равнини, успоредни на равнината Oyz (x=h), получаваме уравненията
от което следва, че за всяко h в сечението се получава насочена надолу парабола, чийто връх лежи върху параболата, определена от уравнения (10).
Нека разгледаме сечения на параболоида с равнини z=h, успоредни на равнината Oxy . получаваме уравненията
или