Алгоритми със структура на вложен цикъл
Всеки цикъл, съдържащ един или повече други цикли вътре в себе си, се наричавложен. Цикълът, който обвива други цикли, се наричавъншен, а останалите цикли се наричат вътрешен. Организационните правила както за външния, така и за вътрешния контур са същите като за обикновен цикъл. Параметрите на тези цикли се променят едновременно, т.е. с една стойност на параметъра на външния цикъл, параметърът на вътрешния цикъл приема всичките си стойности на свой ред.
Матриците са удобен пример за демонстриране на алгоритми с вложен цикъл.
Матрица [A] има M колони и N реда. Всеки елемент от матрицата се определя от два индекса, които показват позицията на този елемент. На първо място се изписва номерът на реда, на второ - номерът на колоната. Например a23 е елемент от матрицата [A], разположен на втория ред на третата колона.
Ако трябва да зададете стойността на матрица, тогава трябва да зададете стойностите на всички нейни елементи. Нека наречем елемента от матрицата aij. За цялата матрица i варира от 1 до N, а j от 1 до M.
Всеки ред от матрицата може да се разглежда като едномерен масив. Въвеждането на първия ред на матрицата определя следния набор от елементи на веригата (фиг. 21).
Схема без блок за модификация
Диаграма с помощта на блок

Същата схема трябва да се използва за втория ред на матрицата, за третия ред и така нататък до M-тия ред. Това означава, че номерът на реда може да бъде даден от цикъл и този цикъл ще бъде външен за цикъла на колоната. Входната диаграма на матрицата [A] без блока за модификация е показана на фиг. 22.
Външен контур за i - блокове 3, 4, 5, 6, 7, 8, 9. Блок 3 - подготовка на цикъла за i. Блок 8 - промяна на параметъра на цикъла. Блок 9 - проверка на условието за край на цикъла. Блокове 4, 5, 6, 7, 8 - тялото на цикъла. Вътрешен контур на j- блокове 4, 5, 6, 7. Блок 4 - подготовка на цикъла за j. Блок 6 - промяна на параметъра на цикъла. Блок 7 - проверка на условието за край на цикъла. Блокове 5, 6 - тялото на цикъла.
При преминаване към следващата стойност i (към следващия ред) j - възстановява първоначалната стойност, равна на 1.

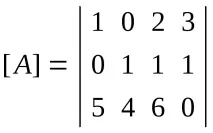
При използване на разработената алгоритъмна схема, елементите на матрицата трябва да бъдат въведени в следния ред: 1, 0, 2, 3, 0, 1, 1, 1, 5, 4, 6, 0.
За да въведете елементите на матрицата по колони (1, 0, 5, 0, 1, 4, 2, 1, 6, 3, 1, 0), трябва да направите цикъла на j външен, а цикъла на i - вътрешен. В този случай вторият индекс се променя по-бавно от първия.
Има задачи, в които няма значение кой параметър да организира външния и вътрешния цикъл. Но има моменти, когато има значение.
При използване на блока за модификация диаграмата изглежда така (фиг. 23).
Проблем.Дадена е квадратна матрица [A], състояща се от N реда и N колони. Намерете сумата от диагоналните елементи.
Разработване на алгоритъм.Изходни данни: брой редове N, брой колони N, елементи на матрицата.
Диагонални елементи на матрицата a11, a22, a33, . , и NN отговарят на условието i=j. Необходимо е да се изброят елементите на матрицата и да се сумират тези, които отговарят на условието i = j.
Блокове 2, 3, 4, 5 - въвеждане на матрицата [A] (виж фиг. 24). Блок 6 - задаване на начална стойност за сумата. Блокове 7, 8 са цикли, които изброяват матрични елементи. Блок 9 - проверка на условието за сумиране. Блок 10 - натрупване на сумата. Блок 11 - теглене на сумата.

Проблем.Група от N души се явиха на M изпити по време на зимната сесия. Известни са резултатите от изпита. Изчислете средния резултат на всеки студент през зимната сесия.
P
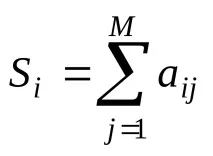
Резултатът от изчислението ще бъде едномерен масив S, състоящ се от N елемента (фиг. 25).
lok 6 - цикъл през редове. В задача i е номерът на ученика в твърдението. Блок 7 - нулиране на сумата. S е променлива, която натрупва сумата от оценките на i-тия студент. Блок 8 - изброяване на предметите от 1 до М. Блок 9 - сумиране на оценките. Блок 10 - определяне на средната стойност. След като цикълът на j завърши, получената сума се разделя на броя елементи. Блокове 11, 12 - изход на едномерен масив.
З