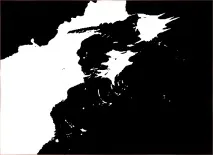
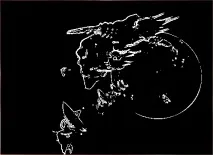
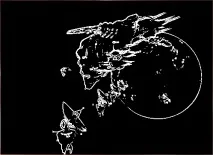
Алгоритми за извличане на контури на изображението

В светлината на последните статии за обработка на изображения, бих искал да говоря малко за алгоритмите за откриване на ръбове: методите на Робъртс, Превит и Собел (тези методи се считат за най-известните и често използвани).

Няма да се занимавам с обемна теория, а ще се огранича само до минималната информация, необходима за разбиране на същността на алгоритмите. Всички тези методи се основават на едно от основните свойства на сигнала за яркост -прекъснатост. Най-често срещаният начин за търсене на прекъсвания е да се обработи изображението с помощта наплъзгаща се маска, наричана ощефилтър, ядро, прозорец или модел, която е вид квадратна матрица, съответстваща на определена група от пиксели в оригиналното изображение. Елементите на матрицата се наричат коефициенти. Работата с такава матрица при всякакви локални трансформации се наричафилтриранеилипространствено филтриране.

Схемата за пространствено филтриране е илюстрирана на фигурата по-долу (вижте Фигура 1).

Снимка 1.Схема на пространствено филтриране

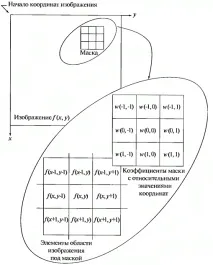
Процесът се основава на просто преместване на филтърната маска от точка на точка в изображението; във всяка точка (x,y) реакцията на филтъра се изчислява с помощта на предварително зададените връзки. В случай на линейно пространствено филтриране отговорът се дава от сумата от произведението на коефициентите на филтъра и съответните стойности на пикселите в областта, покрита от маската на филтъра. За 3x3 елементна маска, показана на фигура 1, резултатът (отговорът)Rот линейното филтриране в точка(x,y)на изображението ще бъде:

(1.1)

което, както можете да видите, е сумата от продуктите на коефициентите на маската и стойностите на пикселите директно под маската. По-специално отбелязвамече коефициентътw(0,0)стои на стойностf(x,y), което показва, че маската е центрирана в точката(x,y).

При откриване на разлики в яркостта се използват дискретни аналози на производни от първи и втори ред. За простота на представянето ще бъдат разгледани едномерни производни.

Първата производна на едномерната функцияf(x)се определя като разликата между стойностите на съседните елементи:

(1.2)

Тук използваме нотация за частни производни, за да запазим същата нотация в случая на две променливиf(x,y), където трябва да работим с частни производни по две пространствени оси. Използването на частична производна не променя същността на съображението.

По същия начин втората производна се определя като разликата между съседни стойности на първата производна:

(1.3)

Изчисляването на първата производна на цифрово изображение се основава на различни дискретни приближения на двуизмерния градиент. По дефиниция градиентът на изображениетоf(x,y)в точката(x,y)е вектор [2]:

(1.4)

Както е известно от курса на математическия анализ, посоката на вектора на градиента съвпада с посоката на максималната скорост на изменение на функциятаfв точката(x,y)[2]. Важна роля при откриването на контури играе модулът на този вектор, който се обозначава с∇fи е равен на

(1,5)

Тази стойност е равна на стойността на максималната скорост на изменение на функциятаfв точка(x,y), а максимумът се достига по посока на вектора∇f. Стойността∇fсъщо често се нарича градиент.

Посоката на градиентния вектор също е важна характеристика. Обозначетеα(x,y)е ъгълът между посоката на вектора∇fв точката(x,y)и остаx. Както е известно от математическия анализ [2],

(1.6)

От тук е лесно да се намери посоката на контура в точката(x,y), която е перпендикулярна на посоката на градиентния вектор в тази точка. И можете да изчислите градиента на изображението, като изчислите частичните производни∂f/∂xи∂f/∂yза всяка точка.

Оператор Робъртс

Нека зоната 3x3, показана на фигурата по-долу (вижте Фиг. 2), представлява стойностите на яркостта в близост до някакъв елемент на изображението.

Снимка 2.3x3 квартал вътре в изображението

Един от най-простите начини за намиране на първите частични производни в дадена точка е да се използва следният оператор за напречен градиент на Робъртс [1]:

(1.7)и(1.8)

Тези производни могат да бъдат реализирани чрез обработка на цялото изображение с оператора, описан от маските на Фигура 3, като се използва процедурата за филтриране, описана по-рано.

Фигура 3.Операторски маски на Roberts

Изпълнението на маски 2x2 не е много удобно, т.к те нямат ясно дефиниран централен елемент, което значително влияе върху резултата от филтрирането. Но това "минус" поражда много полезно свойство на този алгоритъм - висока скорост на обработка на изображения.

Оператор Prewitt

Операторът Prewitt, както и операторът Roberts, работят с областта на изображението 3x3, показана на фигура 2, само използването на такава маска се определя от други изрази:

(1.9)и(1.10)

В тези формули, разликата между сумите в горния и долния ред на квартала 3x3е приблизителна стойност на производната по остаx, а разликата между сумите по първата и последната колона на това съседство е производната по остаy. За прилагане на тези формули се използва оператор, описан с маски на фигура 4, който се нарича оператор Prewitt.

Фигура 4.Маски на Prewitt оператор

Оператор Собел

Операторът Sobel също използва областта на изображението 3x3, показана на фигура 2. Той е доста подобен на оператора Prewitt и модификацията е да се използва коефициент на тежест 2 за средните елементи:

(1.11)и(1.12)

Тази увеличена стойност се използва за намаляване на ефекта от изглаждането чрез придаване на по-голяма тежест на средните точки.

Маските, използвани от оператора Sobel, са показани на фигурата по-долу (виж Фиг. 5).

Фигура 5.Операторски маски Sobel

Обсъдените по-горе маски се използват за получаване на компонентите на градиента. За да се изчисли величината на градиента, тези компоненти трябва да се използват заедно:

(1.14)или(1.15)

Е, в крайна сметка ще демонстрирам резултатите от обработката на изображения (вижте Фигури 6-8) с помощта на описаните методи.