Анализ и решение на задача № 3 OGE по математика
Числени неравенства, координатна права
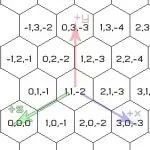
Теория за задача номер 3
За да преобразувате дроби отобикновени вдесетични, е необходимо да извършитеделение на колони.
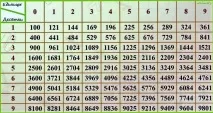
За да изчислите успешно приблизителната стойност на корена, е достатъчно да имате представа за изчислените радикални изрази, а за това трябва да познавате добретаблицата на квадратите на естествените числа !
Таблица на квадратите на естествените числа
В задачи за определяне на знака на израз препоръчвам заместване на числата и пресмятане на израза – подробни указания за този метод са дадени в третия вариант.
Анализ на типични опции за задача № 3 OGE по математика
Първият вариант на заданието
Кое от следните числа е оградено между числата 8/3 и 11/4?
В задача от този тип е необходимо да разделите 8 на 3 и 11 на 4, тоест да преобразувате дробта от обикновена в десетична. Самите дроби може да не са представени в десетична форма, но в нашия случай е достатъчно да разделим само втория знак след десетичната запетая, тъй като отговорът съдържа числа до първия знак след десетичната запетая. И така, нека направим разделението:
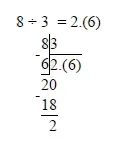
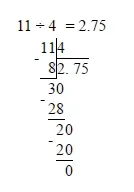
Получаваме стойностите 2.666.. или 2,(6) и 2.75. Разглеждаме вариантите за отговор и избираме съответно първия, тъй като 2,7 е между 2, (6) и 2,75.
Вторият вариант на заданието
На кое от тези числа принадлежиинтервал [ 6 ; 7] ?
За решаването на тази задача е достатъчно да си представим стойностите на числата, по-малки и по-големи от дадено, чиито корени трябва да се изчислят.
- Помислете за √6. √4 е 2, √9 е 3, така че √6 се намира между 2 и 3
- Помислете за √7. Ситуацията е подобна на √6. √4 е 2, √9 е 3, така че √6 се намира между 2 и 3
- Помислете за √38. Най-близкото изчислено число е по-малко от 38 - 36, √36 = 6, най-близкото изчислено число е по-голямо от 38 - 49, √49 = 7, така че √38 се намира между 6 и 7
- Помислете за √50. Най-близкото изчислено число е по-малко от 50 - 49, √49 = 7, най-близкото изчислено число е по-голямо от 50 - 64, √64 = 8, така че √50 се намира между 7 и 8
И така, третият вариант на отговор ни подхожда - √38.
Третият вариант на задачата
Числата a и b са директно отбелязани на координатната права:
Кое от следните твърдения за тези числа не е вярно:
- ab² 0
- a + b 0, тъй като се намира вдясно от нулата и b 0
Така че твърдението е невярно.
Демо версия на OGE 2019
Точка А е отбелязана на координатната линия:
Известно е, че съответства на едно от четирите числа, посочени по-долу. Кое число отговаря на точка А?
Подходът за решаване на този проблем се свежда до визуална оценка на наличните опции на координатната линия, за това е необходимо първо да преобразувате опциите за отговор в приблизителна десетична форма.
Изчисляваме 181/16 - можете да разделите 181 на 16, тогава получаваме 11,3125. Това очевидно е извън определения диапазон, така че тази опция не ни подхожда.
Изчисляваме √37 - най-близката стойност, от която се изчислява квадратният корен, е 36, което означава, че √37 е 6 и нещо друго, което не е необходимо да изчисляваме.Тази стойност е подходяща за нас, тъй като се намира леко вдясно от средата на сегмента 0-10, като точка А.
Нека да разгледаме опцията 0,6 - това е очевидно по-малко от едно, а точка А, както вече разбрахме, се намира в диапазона 5-10. Този вариант не е подходящ за нас.
Вариант 4 също не е подходящ поради горната причина.
Четвъртият вариант
Едно от числата е отбелязано на права линия с точка.
Какво е това число?
Точката, отбелязана на линията, се намира между 2 и 3. Т.е. числото, съответстващо на него, е по-голямо от 1. Това означава, че дробът, който съответства на тази точка, трябва да е неправилен. Но всички дроби, дадени в условието, са неправилни. За да разберете кой от тях е точно на интервала (2; 3), е необходимо да изберете целите им части. Тази от дробите, в която цялата част се оказва равна на 2, е търсеният резултат.
Така че нека го разделим на части:
Цялата част, равна на 2, има две дроби - 1-ва и 4-та. Но нека разгледаме по-отблизо линията. Точката, отбелязана върху него, е близо до деление 3. Нека анализираме дробите, които ни подхождат в този контекст. На първия липсва само 2/11, за да стане равен на 3, докато на четвъртия е само 2/11, отстранен от деленето на 2. Следователно правилният отговор в този случай е дробта 31/11. Съответства на вариант 2.
Пети вариант
На координатната права точки A, B, C и D съответстват на числата -0,201; -0,012; -0,304; 0,021.
Коя точка съответства на числото -0,304?
1) A 2) B 3) C 4) D
Формираме поредица от числа от най-малкото от тях до най-голямото. За целта първо ги разделяме на положителни и отрицателни. И веднага получаваме най-голямото в серията (тъй като то е единственото по-голямо от нула): 0,021.