Булеви алгебри, дискретна математика
Булева алгебра: симетричен полупръстен с унарна операция на допълнение x → x с аксиоми x + x = 1, x x = 0. Уникалност на допълнението. Булеви алгебри и булеви пръстени. Булевата алгебра като решетка. Решетката е алгебра (L, ∨, ∧), в която операциите (обединение на решетката и пресичане) са асоциативни, комутативни, идемпотентни и свързани чрез абсорбционни идентичности a ∨ (a ∧ b) = a, a ∧ (a ∨ b) = a. Всеки симетричен полупръстен е решетка, а разпределителната решетка (всяка операция е разпределителна по отношение на другата) с нула и единица е симетричен полупръстен. Пример за булева алгебра е булевият куб Bn. Теорема: Всяка крайна булева алгебра е изоморфна на булев куб с някакво измерение.
Спомнете си, че по дефиниция булевата алгебра е симетричен полупръстен, в който е въведена още една унарна операция, допълнението. Допълнението към елемент x, означено с x , удовлетворява аксиомите x + x = 1, x x = 0. Забележете, че тези две равенства за всяко x определят елемента x еднозначно, т.е. съществуването на допълнението се определя от свойствата на две двоични операции.
По-подробно можем да кажем, че булевата алгебра е универсална алгебра от формата (L, ), която отговаря на следните условия:
а) всяка двоична операция е комутативна, асоциативна, идемпотентна и има неутрален елемент;
б) всяка двоична операция е разпределителна по отношение на другата;
в) неутралния елемент на всяка двоична операция анихилира друга двоична операция;
г) събирането е свързано с двоичните операции чрез аксиомите x + x = 1, x x = 0.
И двете операции генерират две отношения на ред, които са взаимно обратни. Така връзката x y, която е еквивалентна на равенството x + y = y, също се определя от равенството xy = x.
Ако в булевата алгебра B въведемоперация x ⊕ y = x y + x y, тогава получаваме алгебрична система (L, ), която е пръстен с единица, в която операцията умножение е идемпотентна (булев пръстен). Накратко, булевата алгебра е булев пръстен. Обратно, във всеки булев пръстен (L, ) умножението е комутативно и събирането удовлетворява условието x⊕x=0. Поставяйки x+y=x⊕y⊕xy, x =x+1, получаваме алгебрична система (L, ), която е булева алгебра.
Към концепцията за булева алгебра може да се подходи и от друг ъгъл. Комутативна идемпотентна полугрупа се наричаполурешетка. В полурешетка (както и в полупръстен) може да се въведе релация от естествен ред съгласно правилото x y ⇔ x+y = y. Обратно, всяко подредено множество, в което всяко множество от два елемента има най-малка горна граница, може да се интерпретира като полурешетка с операцията x + y = sup. Ако в едно подредено множество всяко двуелементно множество има както най-добрата горна, така и долната граница, тогава структурата на полурешетката може да бъде въведена в това множество по два начина: с операцията sup и с операцията inf. Първата структура се нарича горна полурешетка, а втората - долна. Двете операции на решетката са свързани чрез идентичностите
Алгебра (R, ), за която (R, ∨) и (R, ∧) са полурешетки и операциите са свързани чрез абсорбционни идентичности a ∨ (a ∧ b) = a, a ∧ (a ∨ b) = a, се нарича решетка. Бинарните операции се наричат решетъчни операции (обединение на решетка и пресичане на решетка). Решетъчните операции влизат в структурата на решетката симетрично. Следователно всеки от тях може да се нарече съюз, тогава вторият ще бъде пресечна точка. Всяко подредено множество има решетъчна структура, в която за всеки набор от два елемента има най-добра горна и най-добра долна граница. В този случай решетъчните операции са a∨b=sup и a∧b=inf.
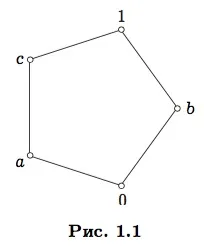
Всеки симетричен полупръстен има решетъчна структура. Решетката в общия случай може да не е симетричен полупръстен. Например петоъгълникът е подредено множество с връзка на реда, дадена от диаграмата на Хасе* на фиг. 1.1 е решетка, но в тази решетка операциите не са разпределителни една спрямо друга, както би трябвало да са в симетричен полупръстен. Обаче всяка разпределителна решетка (т.е. решетка, в която всяка операция е разпределителна по отношение на друга) с нула и единица (елементи на неутрално обединение и пресичане) е симетричен полупръстен.
Най-простият пример за булева алгебра е двуелементна булева алгебра
с операции x+y = max, xy = min, x = x+1. Обобщение на този пример е булевата алгебра B n с покомпонентно изпълнение на операциите на алгебра B върху кортежи. Алгебрата B n се нарича n-та декартова степен на B или n-мерен булев куб. Оказва се, че всяка крайна булева алгебра е изоморфна на някакъв булев куб. Просто казано, няма други примери за крайни алгебри освен булевия куб.
Друг важен пример за булева алгебра е алгебрата SA = 2 A , , т.е. множеството от всички подмножества на множеството A с теоретико-множествените операции обединение, пресичане и събиране. Обърнете внимание, че всички практически значими примери за булеви алгебри могат да бъдат интерпретирани по отношение на алгебрата SA или някои от нейните подалгебри. Например, елементите на булевата алгебра B n (n-мерни булеви вектори) могат да се разглеждат като запис на характеристичната функция на подмножество в набор от n елемента. И тогава операциите в B n ще съответстват на теоретико-множествените операции. Симетричният полупръстен ([a, b], ) може да се трансформира в алгебра на множествата, като на всеки x ∈ [a, b] се присвои отсечката [a, x]. Няколкотакива сегменти е затворен при операциите на обединение и пресичане, т.е. образува подалгебра в 2 [a,b] . Вярно е, че този полупръстен не е булева алгебра, тъй като е невъзможно да се въведе операцията за добавяне в него.