Числа, които характеризират графиката - Studiopedia

Цикломатичното число на граф е числото u=N-n+p, където N е броят на ръбовете на графа, n е броят на неговите върхове, P е броят на свързаните компоненти. За свързан график u=N-n+1.

Теорема. Цикломатичното число на графика е равно на най-големия брой независими цикли.

Концепцията за независими цикли е следната. Нека свържем цикъла μ на графиката G с някакъв вектор. За да направим това, даваме на всеки ръб на графиката произволна ориентация. Ако цикълът μ преминава през ръба uk в посоката на неговата ориентация rk пъти и в обратната посока Sk пъти, тогава задаваме c k =rk-Sk. Вектор с 1 ,c 2 ,…,c K ,…,c N ) от N-мерно пространство се наричавекторен цикъл, съответстващ на цикъла μ. Циклите μ1, μ2,… се наричат независими, ако съответните вектори , ,… са линейно независими.

Следните твърдения са следствие от разглежданата теорема:

1. Свързана графа G няма цикли тогава и само ако u=0. Такъв граф е дърво (различни дефиниции на дървовиден граф ще бъдат обсъдени в специален раздел 3.2).

2. Свързан граф G има уникален цикъл тогава и само ако u=1.

Цикломатичното число на свързан граф може да се дефинира като броя на ребрата, които трябва да бъдат премахнати, за да стане графиката дърво.

Цикломатичното число на графиката, показана на фиг. 3.1.10 е равно на 3.

Числото на вътрешната стабилност на графиката. Нека е дадена някаква графика G(x, r x). Да разгледаме подмножество от неговите върхове S X, в което всеки две точки не са съседни. Такова подмножество S се нарича вътрешно стабилно. С други думи, подмножество S X е вътрешно стабилно, ако rSÇS=ø.

Означаваме с S мощността на множеството S. Нека F е множеството от всички вътрешно стабилни множества.Вътрешното число на стабилност на графика G е

a(G)=S.

Намирането на a(G) трябва да започне с максималния брой върхове и, постепенно увеличавайки го, да провери дали избраните върхове образуват вътрешно стабилно множество.

Но ако добавим към някой от тези набори някакъв връх, който не се съдържа в него, тогава подмножеството ще престане да бъде вътрешно стабилно, следователно a(G3)=2.

Броят на външната стабилност на графиката. Нека е дадена някаква графика G(x, rx). Подмножество от неговите върхове TÍX е външно стабилно множество, ако за всяка точка xiÎ(X/T) условието

Нека T е мощността на множеството T. Нека Ф е множеството на всички външно устойчиви множества. Външното число на стабилност на графика G е

b(G)=T.

Когато изчислявате числото на външна стабилност, трябва да започнете с максималния брой върхове на графиката, след това да го намалите, като проверите дали избраните върхове образуват външно стабилно множество.

Нека определим броя на външната стабилност за графиките, показани на фиг.3.1.11. Всяка двойка върхове на графа G1 образува външно стабилно множество, но нито един от неговите върхове не е външно стабилно множество, следователно b(G1)=2. Графиката G2 съдържа две външно стабилни множества T1=1,x3>, T2=2,x4> с минимален брой елементи, т.е. b(G2)=2. За графиката G3, външно стабилният набор от минимална мощност е T=1,x3>, т.е. b(G3)=2.

Проблемът с часовите се свежда до определяне на външното число на стабилност на графика. Стражите се поставят на поста, който охранява n обекта, като един и същ часовой може да наблюдава няколко обекта. Трябва да разберете какъв е минималният брой часови, необходими за наблюдение на всички обекти. Графът, показан на фигура 3.1.12, отговаря на следния проблем: 9 върхаграфика - охранявани обекти (n=9), ръбовете характеризират възможността за гледане на обекти от часови. Така например, часовият на обект X1 може едновременно да наблюдава обекти X2,X3,X4, X9, часовият на обект X2 може едновременно да наблюдава обекти X1,X3,X7,X8 и т.н. За тази графика числото на външна стабилност е 2. Външно стабилното множество се формира от върховете X4,X8. Двама часови, разположени в точки X4 и X8, са достатъчни за охрана на всички обекти.

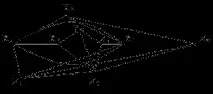
Ядрото на графиката. Ако наборът от върхове на графа G(x, rx) съдържа подмножество LÍX, което е както вътрешно, така и външно стабилно, тогава такова подмножество L се наричаядро на графа.

Означаваме с L мощността на множеството L. Тази величина удовлетворява неравенството a(G)³L³b(G).

Хроматично число на графа.Да предположим, че всеки връх на графа G е оцветен в някакъв цвят, така че два съседни върха да не са оцветени еднакво. Ако това изисква K цвята, тогава графиката се нарича хроматична от ред K. Минималният брой K, за който графиката остава хроматична, се нарича хроматично число и се обозначава с γ. За графиката G, показана на фигура 3.1.13, хроматичното число γ(G)=3.

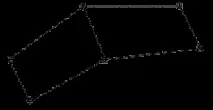
Теорема. За всяка графика G е в сила неравенството n£a(G)g(G), където n=X е кардиналността на множеството X, a(G) е вътрешното число на стабилност, а g(G) е хроматичното число на графиката.

Доказателство. Целият набор от върхове на графа може да бъде разделен на g вътрешно стабилни комплекта, състоящи се от точки от един и същи цвят. Нека вътрешно стабилните множества съдържат m1,…,mg върхове. mi£a(G), защото a(G) по дефиниция е максималният брой върхове на вътрешно стабилни множества. Но n=m1+m2+...+mg, следователно n£a(G)g(G).

Проблемът с оцветяването на геометрична карта е свързан с определянето на хроматичното число на графика.Всяка географска карта може да бъде представена като граф G(x, rx), където върховете са държавите, а ръбовете са страните, граничещи една с друга. Такава графика е планарна. Хипотезата за четири цвята се състои в твърдението, че графиката, съответстваща на всяка географска карта, има хроматично число най-много 4. Дълго време това предположение остава недоказано, въпреки широкия интерес на математиците към този проблем. Благодарение на създаването на съвременни компютри, решението на този проблем стана възможно, което беше направено от американските математици К. Апел и У. Хакен. Проблемът беше решен чрез свеждането му до някои конкретни въпроси от чисто аритметичен характер, изискващи голям брой изчисления, които биха били извън силите на човек, който не е въоръжен с модерни компютърни технологии.

Не намерихте това, което търсихте? Използвайте търсачката:

Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо