Ефирна формула
Разгледайте интерференцията в плоскопаралелна плоча, ще вземем предвид лъчите, които претърпяват многократни отражения (фиг. 1). Нека коефициентът на отражение (частта от енергията на падащата светлина, която се връща в отразения лъч) на светлината от границата на плочата с въздуха е $\rho .$ Ако няма поглъщане на енергия, тогава частта от енергията, която преминава през интерфейса, е $(1-\ \rho )$. В случай, че има въздух от двете страни на плочата (една и съща среда), тогава коефициентите на отражение са еднакви.
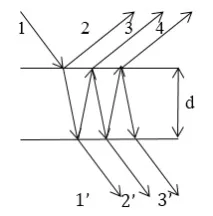
Приемаме, че монохроматична светлина пада върху плочата, нейният интензитет е равен на $I_0$. В този случай интензитетите на лъчите $1',2',3',\dots $ са съответно равни:
В този случай съответните реални амплитуди:
където $a_0$ е амплитудата на падащата вълна. Разлика в пътя между два съседни интерфериращи лъча:
където $\varphi $ е ъгълът на падане на лъча върху повърхността.
Фазовата разлика ($\delta $) в този случай ще бъде:
Амплитудата на вълната, преминала през плочата, може да бъде представена като намаляваща геометрична прогресия:
Опитайте да помолите учителите за помощ.
В случай, че плочата е дълга, тогава ние считаме прогресията за безкрайна, следователно:
Използвайки израз (6), записваме формулата за интензитета на предаваната вълна:
Нека намерим интензитета на отразената вълна ($I_r$). Интензитетът на отразените лъчи (1,2,3. ) може да се изрази като:
В този случай съответните реални амплитуди са равни:
където минусите във формулите за амплитудите отчитат загубата на половината вълна при отражение от повърхността на плочата. В този случай лъч $2$ се отразява от границата въздух-плоча (стъкло), всички останали отражения възникват на границата стъкло-въздух. Общата амплитуда на отразената вълна е представена отекспоненциално:
В този случай изразът за интензитета на получената отразена вълна има формата:
Формули (7) и (11) се наричат формули на Ейри.
Последици от формулите на Airy
Ако считаме, че поглъщането на светлина от средата не се извършва, тогава равенството е изпълнено:
Моделите на разпределение на интензитета в пропуснатата и отразената светлина се допълват взаимно, което означава, че максимумите на единия модел съответстват на минимумите на другия. За да се получи интерференчна картина, трябва да се използва дълъг източник на светлина. В този случай интерферентните ивици ще бъдат ивици с еднакъв наклон. Те могат да бъдат сглобени с леща върху екран, който е поставен във фокалната равнина. Интерферентните ивици ще бъдат под формата на концентрични пръстени, центрирани в точката на сближаване на лъчите, перпендикулярни на повърхността на плочата.
Задайте въпрос на експерти и получете отговор за 15 минути!
Максимумите в пропуснатата светлина се получават при $\delta =2\pi m\ \left(където\ m е цяло число\ \right).\ $В отразената светлина това е минималното условие.
Многостранната интерференция се реализира в дебели плочи, следователно, за да се получи интерференчен модел, е необходимо да се използва светлина с висока монохроматичност. Методите на интерферентната спектроскопия се използват за изследване на структурата на тънките спектрални линии. Интерферентните спектроскопи имат висока разделителна способност с просто устройство, ниска цена и лесна употреба.
Покажете, че от формулите на Airy следва, че при липса на абсорбция $I_0=I_r+I_l$.
Решение:
Нека запишем формулите на Airy за интензитета на пропуснатата светлина ($I_l$):
Нека директно сумираме тези изрази:
Q.E.D.
Каква е разликата между разпределението на интензитетас многопътна интерференция, ако индексът на отражение е много малък ($\rho \ll 1$) и ако клони към единица.
Решение:
Нека определим какво е разпределението на интензитета за интерференция на многолъчева светлина, ако коефициентът на отражение е много малък. Нека напишем формулата на Airy за интензитета на пропуснатата светлина ($I_l$):
за $\rho \ll 1$, разпределението на интензитета във вълната, предавана през плочата, ако $^2$ се пренебрегне, и разширението в $\ \rho $ може да бъде представено като:
\[I_l=1-4s^2\left(\frac\right)=1-2s\left(1-cos \delta \right)\left(2.2\right).\]
Ето формулата на Airy за интензитета на отразената светлина:
като вземем предвид $\rho \ll 1,$ ще извършим операции, подобни на тези, които направихме по-рано, получаваме:
\[I_r=4\rho ^2\left(\frac\right)=2\rho \left(1-cos\delta \right)\left(2.4\right).\]
Разпределението на интензитета се определя от условия, подобни на тези на проста двулъчева интерференция. Като че ли не се вземат предвид многократните отражения.
Разпределението на интензитета се променя значително, ако коефициентът на отражение се увеличи, особено ако е близо до единица. В този случай почти цялата светлина е концентрирана в тесни интерферентни ивици на тъмен фон. При отразена светлина се получават същите остри тъмни ивици на интерферентната картина. Числителят във формула (2.1) е постоянен. При максимум (за $\delta =2\pi m$) $I_=I_0.$
Не сте намерили отговора на вашия въпрос?
Просто напишете за какво имате нужда от помощ