еластични вълни
§ 1.Разпространение на вълната в еластична среда
Ако в някое място на еластична (твърда, течна или газообразна) среда се възбудят вибрации на нейните частици, тогава поради взаимодействието между частиците тази вибрация ще се разпространява в средата от частица към частица с определена скоростυ.Процесът на разпространение на вибрации в пространството се нарича вълна.
Частиците на средата, в която се разпространява вълната, не са въвлечени от вълната в постъпателно движение, те само осцилират около своите равновесни положения. В зависимост от посоката на трептенията на частиците по отношение на посоката на разпространение на вълната се разграничават надлъжни и напречни вълни. При надлъжна вълна частиците на средата осцилират по посока на разпространение на вълната. При напречна вълна частиците на средата осцилират в посоки, перпендикулярни на посоката на разпространение на вълната. Еластични напречни вълни могат да възникнат само в среда с устойчивост на срязване. Следователно в течни и газообразни среди могат да възникнат само надлъжни вълни. В твърда среда могат да възникнат както надлъжни, така и напречни вълни.
На фиг. Фигури 1.1 и 1.2 показват вибрации на частици, чиито равновесни позиции лежат на остаx.. Разпространявайки се от източника на вибрации, вълновият процес обхваща все нови и нови части от пространството. Геометричното място на точките, до които достигат флуктуациите към момента на времетоt,се нарича фронт на вълната (или фронт на вълната). Фронтът на вълната е повърхността, която разделя часттапространство, вече въвлечено във вълновия процес, от областта, в която още не са възникнали трептения.
Географското място на точките, осцилиращи в една и съща фаза, се нарича вълнова повърхност. Вълновата повърхност може да бъде начертана през всяка точка от пространството, обхванато от вълновия процес. Следователно има безкраен брой вълнови повърхности, докато във всеки момент има само един вълнов фронт. Вълновите повърхности остават неподвижни. Вълновият фронт се движи постоянно.
Вълновите повърхности могат да бъдат с всякаква форма. В най-простите случаи те имат формата на равнина или сфера. Съответно вълната в тези случаи се нарича плоска или сферична. При плоска вълна вълновите повърхности са набор от равнини, успоредни една на друга; при сферична вълна те са набор от концентрични сфери.
Да разгледаме случая, когато плоска вълна се разпространява по остах.Тогава всички точки на средата, чиито равновесни положения имат една и съща координатах(но различни координатиyиz), трептят в една и съща фаза.
Разстояниетоλ, през което вълната се разпространява за време, равно на периода на трептене на частиците на средата, се нарича дължина на вълната. Очевидно е, чекъдетоυ—скорост на вълната,T—период на трептене. Дължината на вълната може да се определи и като разстоянието между най-близките точки на средата, осцилираща с фазова разлика, равна на 2p (виж фиг. 1.3).
§ 2.Уравнения на равнинни и сферични вълни
Вълновото уравнение е израз, който дава изместването на осцилираща частица като функция на нейните координатиx,y,zи времеt:
x=x(x,y,z,t)(има предвид координатите на равновесното положение на частицата). Тази функция трябва да бъде периодична както по отношение на времетоt, така и по отношение на координатитеx, y,z.. Периодичността в координатите следва от факта, че точките, разделени една от друга на разстояниеλ, осцилират по един и същи начин.
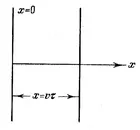
Нека намерим формата на функциятаx,в случай на плоска вълна, като приемем, че трептенията са хармонични. За да опростим, нека насочим координатните оси така, че остаxда съвпада с посоката на разпространение на вълната. Тогава вълновите повърхности ще бъдат перпендикулярни на остаxи тъй като всички точки на вълновата повърхност осцилират еднакво, изместванетоxще зависи само отxиt:x=x(x,t).Нека флуктуациите на точките, лежащи в равнинатаx= 0 (фиг. 2.1) имат формата
Нека намерим вида на трептене на точки в равнината, съответстващи на произволна стойностx.За да премине от равнинатаx= 0 до тази равнина, вълната се нуждае от времеt=x/υ(υе разпространението на вълната скорост на движение). Следователно, трептенията на частиците, лежащи в равнинатаx, ще изостават във времето сtот трептенията на частиците в равнинатаx= 0, т.е. те ще имат формата
И така, уравнението на плоска вълна (както надлъжна, така и напречна), разпространяваща се впосоката на остаx,е както следва:
x=acos [w( t −x/υ )+a]Стойносттаaпредставлява амплитудата на вълната. Началната фаза на вълнатаaсе определя от избора на началотоxиt.Когато се разглежда една вълна, началото на времето и координатите обикновено се избират така, чеaда е равно на нула. Когато разглеждаме няколко вълни заедно, обикновено е невъзможно началните фази да бъдат равни на куршум за всички тях.