Физически приложения на повърхностните интеграли
Център на масата и инерционни моменти на черупката;
Сила на привличане и сила на натиск;
Потокът на течност и материя през повърхността;
Електрически заряд, разпределен по повърхността;
Електрически полета (теорема на Гаус в електростатиката).
Нека разпределението на масата \(m\) в тънка обвивка се описва от непрекъсната функция на плътност \(\mu \left( \right).\) = \frac>>>,>\;\; = \frac>>>,> \] където \[ > = \iint\limits_S\right)dS> ,>\;\; > = \iint\limits_S\right)dS> ,>\;\; > = \iint\limits_S\right)dS> > \] - така нареченитемоменти от първи ред по отношение на координатните равнини\(x = 0,\) \(y = 0\) и \(z = 0,\), съответно.
Инерционните моменти на обвивката около осите \(Ox, Oy, Oz\)се изразяват съответно с формулите \[ = \iint\limits_S + > \right)\mu \left( \right)dS> ,>\;\; = \iint\limits_S + > \right)\mu \left( \right)dS> ,>\;\; = \iint\limits_S + > \right)\mu \left( \right)dS> .> \]Инерционните моменти на черупката спрямо равнините \(xy, yz, xz\)се определят по формулите \[ > = \iint\limits_S \mu \left( \right)dS> ,>\;\; > = \iint\limits_S \mu \left( \right)dS> ,>\;\; > = \iint\limits_S \mu \left( \right)dS> .> \]
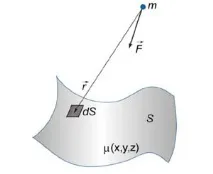
Силата на привличанемежду повърхността \(S\) и точковото тяло \(m\) се определя от израза \[\mathbf = Gm\iint\limits_S \right)\frac>>>dS> ,\] където \(\mathbf = \left( ,y - ,z - > \right),\) \(G\) е гравитационната константа, \( \right)>\) е функцията на плътността.
Да предположим, че повърхността \(S\) е дадена от вектора \(\mathbf\) и се влияе отнякаква сила на натиск (може да бъде язовир, крило на самолет, стена на цилиндър със сгъстен газ и др.). Общата сила \(\mathbf,\), създадена от натиск \(p\left( \mathbf \right),\) се намира с помощта на повърхностния интеграл \[\mathbf = \iint\limits_S \right)d\mathbf> .\] Налягането, по дефиниция, действа в посоката на нормалния вектор на повърхността \(S\) във всяка точка. Следователно можем да запишем \[\mathbf = \iint\limits_S \right)d\mathbf> = \iint\limits_S dS> ,\] където \(\mathbf\) е единичният нормален вектор към повърхността \(S.\)
Ако скоростта на флуида \(\mathbf\left( \mathbf \right),\) се разглежда като векторно поле, тогава потокът през повърхността \(S\) се наричафлуиден поток. Той е равен на обема течност, преминаваща през повърхността \(S\) за единица време и се изразява с формулата \[\Phi = \iint\limits_S \left( \mathbf \right) \cdot d\mathbf> .\] По подобен начин потокът на векторно поле \(\mathbf = \rho \mathbf,\), където \(\rho\) е плътността, се наричапоток на материятаи се определя от израза \[\Phi = \iint\limits_S \left( \mathbf \right) \cdot d\mathbf> .\] Числено е равна на масата материя, преминаваща през повърхността \(S\) за единица време.
Потокът на електрическо изместване\(\mathbf\) през затворена повърхност \(S\) е равен на алгебричната сума на всички заряди, разположени вътре в повърхността: \[\Phi = \iint\limits_S \cdot d\mathbf> = \sum\limits_i > ,\] където \(\mathbf = \varepsilon \mathbf,\) \(\mathbf\) е напрегнатостта на електрическото поле, \(\varepsilon\) е относителната диелектрична проницаемост на средата, \( = 8,85 \пъти >\,\text\) е диелектричната проницаемост на вакуума.
Теоремата на Гаус е приложима за всякакви затворени повърхности. В случай на повърхност с достатъчна симетрия товатеоремата опростява изчисляването на електрическото поле. Теоремата на Гаус се счита за един от основните постулати на теорията на електричеството. Включен е в системата от основни уравнения на Максуел.
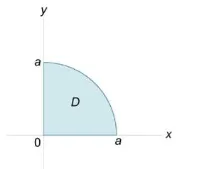
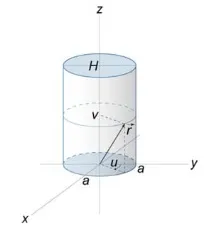
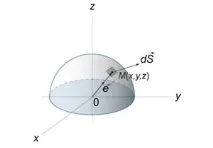
Изчислете момента на първия ред \(>.\) \[ > = \iint\limits_S\right)dS> > = \iint\limits_S > = \iint\limits_\right)> >>> \десен)>^2> +>>> \right)>^2>> dxdy> ,> \] където проекцията \( \right)>\) на повърхността върху равнината \(xy\) е частта от окръжността, разположена в първия квадрант (фигура \(4\)).
И така, координатите на масовия център на черупката са \[\left( ,,> \right) = \left( ,\frac,\frac> \right).\]
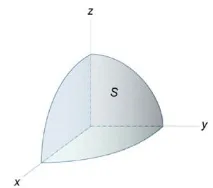
Инерционният момент \(\) се намира по формулата: \[ = \iint\limits_S + > \right)\mu \left( \right)dS> > = \iint\limits_S + > \right)dS> ,> \] където повърхността \(S\) е полукълбото \( + + = 1\;\наляво( \вдясно).\)
Да разгледаме точка \(M\left( \right)\) от полукълбото, която принадлежи на малък участък от повърхността \(dS\) (фигура \(5\)). Силата на привличане \(d\mathbf\left( M \right)\) между повърхностен елемент \(dS\) и маса \(m\) може да бъде записана като \[d\mathbf\left( M \right) = \fracmdS>>>>\mathbf\left( \right),\] където \(G\) е гравитационната константа, \(\mathbf\left( \right)\ ) е единичният вектор, насочен от точка \(O\) към точка \(M.\) Тъй като \(\mathbf\left( \right) = \left( \normalsize, \large\frac\normalsize, \large\frac\normalsize> \right),\) можем да запишем \[d\mathbf\left( M \right) = \fracmdS>>> ;>\left( \right).\] След интегриране по повърхността на полукълбото получаваме следните изрази за компонентите на силата на привличане: \[ = \fracm>>>>\iint\limits_S ,>\;\; = \fracm>>>>\iint\limits_S ,>\;\; =\fracm>>>>\iint\limits_S .> \] В сферични координати уравнението на полукълбо се записва като \[ \left( \right) > = + r\sin \psi \sin \theta \cdot \mathbf + r\cos \theta \cdot \mathbf,> \] където \(0 \le \psi \le 2\pi ,\;0 \le \theta \le \large\frac\normalsize.\)
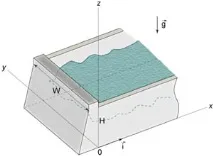
При условия на хидростатично равновесие налягането върху повърхността на язовира зависи от координатата \(z\) в съответствие с формулата \[p\left( z \right) = \rho g\left( \right),\] където \(\rho\) е плътността на водата, \(g\) е гравитационното ускорение.
Общата сила на натиск, действаща върху бента, ще бъде \[ = \iint\limits_S dS> > = \right) \cdot \left( < - \mathbf> \right)dydz> > > = > \right)\left[>>> \вдясно)> \right_0^H> \right] > = >>\left( < - \mathbf> \right).> \] Векторът \(\left( < - \mathbf> \right)\) показва посоката на силата \(\mathbf.\) Абсолютната стойност на силата е \[\left \mathbf \right = \frac>>.\]
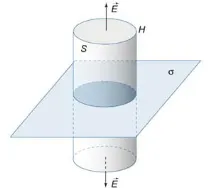
Поради симетрията на системата, векторът на напрегнатостта на електрическото поле трябва да бъде перпендикулярен на повърхността, а големината на силата трябва да бъде еднаква във всички точки, еднакво отдалечени от плочата.
Помислете за условна гаусова повърхност под формата на цилиндър с напречно сечение \(S\) и височина \(2H\) (фигура \(8\)). Електрическият поток на изместване е различен от нула само в основите на цилиндъра. Следователно \(\Phi = 2ES,\), където \(E\) е електрическото поле в основите на цилиндъра. Общият заряд вътре в цилиндричната повърхност е равен на \(Q = \sigma S.\) Тогава, по теоремата на Гаус, получаваме \[ \iint\limits_S = Q,>\;\; ES = \сигма S\;\;\текст\;\;> >>.> \]