Формули на динамиката, курсове

Вземетебезплатен курс по основна математика. Тези знанияса необходими за решаване на задачи по физика.
Векторна алгебра от нулата!

Вземетебезплатенкурс по векторна алгебра. Той енеобходимза решаване на задачи по физика.
Книги за изучаване на физика и за подготовка за изпит

Динамични формули
Материална точка (точкова маса) е геометрична точка, надарена с маса.
Твърдото тяло е набор от материални точки, разстоянието между които остава постоянно през цялото време.
Еластично тяло е тяло, в което при деформиране възникват еластични сили.
Първият закон на Нютон. В инерционните системи тялото поддържа състояние на покой или равномерно и праволинейно движение, докато други тела или действат върху него, или, ако действат, тогава по такъв начин, че тези действия се компенсират взаимно.
Втори закон на Нютон. В инерционните референтни системи големината на ускорението, получено от тялото в резултат на некомпенсираното действие на други тела върху него, е право пропорционална на големината на получената сила и обратно пропорционална на масата на тялото, върху което е направено това некомпенсирано въздействие. Посоката на резултантното ускорение съвпада с посоката на резултантната сила. Математически това твърдение може да се напише по следния начин:
а =F /m,
къдетоa - ускорение на тялото, m - маса на тялото,F - резултантната сила, действаща върху това тяло от други тела. Така че, ако разглежданото тяло взаимодейства с тела 1, 2, 3 и т.н., тогава силитеF 1,F 2,F 3 и т.н. ще действат върху него от тези тела. В такъв случай
F =F 1 +F 2 +F 3 + и т.н.
Третият закон на Нютон. АкоF 1.2 е силата, действаща на първото тяло от второто, аF 2.1 е силата, действаща на второто тяло от първото, тогава тези сили са равни по големина и са насочени в противоположни посоки. Математически това се записва така:
F 1,2 = −F 2,1.
Трябва да се има предвид, четези закони се спазват стриктно само за материални точки (също както на страницата "Кинематика", за удобство на представянето понякога ще наричам материална точка тяло, обект, частица. Така че не се обърквайте от факта, че в горните закони се появява тяло, ние, разбира се, говорим за точкови маси).
Закон за гравитацията:
където F е модулът на силата, с който телата с маси m1 и m2 се привличат едно към друго,
γ \u003d 6,67259 10 −11 m 3 / kg s 2. Тази величина се нарича гравитационна константа. Законът за всемирното притегляне се спазва стриктно и за материалните точки.
Импулс (импулс)p на тяло е произведението на масата m на тялото и неговата скоростv, т.е.
p = mv.
Инерцията е вектор! Тази концепция е приложима както за материална точка, така и за тяло, движещо се постъпателно (ако тялото не се движи постъпателно, а по някакъв друг начин, тогава понятието за скоростта на тялото като такова, а оттам и неговия импулс, не съществува).
Импулсът на система от материални точки или система от тела, движещи се прогресивно, е векторната сума на импулсите на всички обекти, които съставят системата. Така че, ако системата се състои от обекти с маси m1, m2, m3 и т.н., имащи съответно скоростиv 1,v 2,v 3 и т.н., тогава импулсът на системата
P = m1v 1 + m2v 2 + m3v 3+ и т.н.
Елементарен импулс на сила (да не се бърка с импулс, т.е. количеството на движение натяло ) е произведение на силаF и безкрайно малък интервал от време dt на нейното действие, т.е.F dt. Силовият импулс няма специално обозначение. През интервала dt силата остава практически постоянна.
Законът за промяна на импулса на материална точка (тяло) в диференциална форма:
dp =F dt,
безкрайно малка промяна в импулса на материална точка (или прогресивно движещо се тяло) е равна на елементарния импулс на силата, действаща върху частицата (тялото).
Законът за запазване на импулса на материална точка (тяло) :
dp = 0 илиp = const,
това означава, че импулсът на частица (или транслационно движещо се тяло) не се променя по време на движението. Това е възможно, ако върху частицата (тялото) не действат външни сили (или действат, но резултантната им е нула).
Законът за промяна на импулса на система от материални точки (тела, движещи се напред) в диференциална форма:
dP =F (e) dt,
къдетоF (e) е резултантната външна сила, действаща върху системата.
Законът за запазване на импулса на система от материални точки (тела, движещи се напред) :
d3>P = 0 илиP = const.
Това е възможно, акоF (e) = 0. Система, за коятоF (e) = 0, се наричазатворена илиизолирана.
Елементарна работа dA на силаFвърху безкрайно малко преместване dr е скаларното произведение на сила и безкрайно малко преместване, т.е.
dA =F dr.
При това изместване силата практически не се променя.
Работата на гравитацията. Когато тяло падне от височина h1до височина h2
A = mg(h1 − h2). Работата в този случай е положителна, тъй като h1 е по-голямо от h2. При повдигане на тялото от височина h2 до височина h1
В този случай работата е отрицателна, тъй като h2 е по-малко от h1. В тези формули m е масата на тялото, g е ускорението на гравитацията (гравитационно ускорение).
Работата на гравитационната сила, когато разстоянието между два взаимодействащи обекта намалява от r1 до r2:
където γ е гравитационната константа, M и m са масите на обектите. Формулата е валидна за точкови маси.
Кинетична енергия Tматериална точка :
Потенциална енергия Uгравитационно взаимодействие на две частици с маси m и M, разположени на разстояние r една от друга:
Обща механична енергия Eчастици :
Законът за промяна на кинетичната енергия на частиците в диференциална форма:
тоест елементарната работа на сила, действаща върху материална точка, е равна на елементарно (безкрайно малко) изменение на нейната кинетична енергия.
Законът за запазване на кинетичната енергия на частиците в диференциална форма:
dE = 0 или E = const,
Това е възможно, ако върху частицата не действат сили или действат, но общата им работа е нула.
Законът за промяна на общата механична енергия на частица в диференциална форма:
това означава, че една безкрайно малка промяна в общата механична енергия на частицата е равна на елементарната работа на резултата от всички външни сили, действащи върху частицата.
Кинетичната енергия Tна система от материални точки е стойност, равна на сумата от кинетичните енергии на всички елементи на системата, т.е.
Законът за промяна на кинетичната енергия на система от частици в диференциална форма:
т.е. безкрайно малъкпромяната в кинетичната енергия на система от частици е равна на елементарната работа на всички (!) Сили, действащи върху всички елементи на системата по време на елементарното движение на тези елементи.
Общата потенциална енергия Uна отворена система (или просто потенциалната енергия на отворена система):
Uint - вътрешна (или собствена) потенциална енергия на системата. При въвеждането на тази концепция се пренебрегват взаимодействията на елементите на системата с външни обекти, т.е. системата се счита за изолирана. Трябва да се има предвид, че собствената потенциална енергия на системата е неадитивна величина, т.е. в общия случай тя не е равна на сумата от собствените потенциални енергии на частите на системата, тъй като е необходимо да се вземе предвид и потенциалната енергия на взаимодействие Uvz на отделните части на системата, т.е.
Un - собствена потенциална енергия на n-та част от системата.
Uext е общата потенциална енергия на елементите на системата в общото поле на всички външни потенциални сили.
Общата механична енергия Eна отворена система от материални точки е сумата от потенциалната енергия U на системата и общата кинетична енергия T на всички елементи на системата в даден момент, т.е.
Законът за изменение на общата механична енергия на системата в интегрална форма. Промяната в общата механична енергия на системата ΔE от материални точки е равна на общата работа Anepot, произведена върху системата от всички непотенциални сили (както вътрешни, така и външни), тоест ΔE = Anepot.
Законът за запазване на пълната механична енергия на система от материални точки в интегрална форма. Общата механична енергия на всяка система от материални точки (както затворена, така и отворена) се запазва, ако общата работа, извършена върху системата от всички непотенциални сили, е равна нанула, т.е. ΔE = 0, ако Anepot = 0.
Момент M на сила F спрямо точка O :
M = [r,F ],
къдетоr е радиус векторът, начертан от точка O до точката на прилагане на силаF.
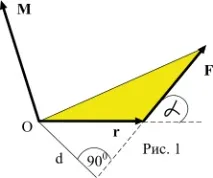
Модулът на момента на силата се определя от израза:
където r·Sin α = d е рамото на силата (перпендикулярно от точка O към линията на действие на силата).