Франсис Хил OpenGL
където u и v, както обикновено, варират от 0 до 1. Пример за такъв пластир е показан на фиг. 11.54. Всеки ^-контур, например, за v = v0, е крива на Безие по отношение на u, базирана на четири контролни точки Pk(v0), които сами по себе си лежат по протежение на квадратични криви на Безие. (Как се описва всеки s-контур?) Всички 12 PiV контролни точки образуват контролен полиедър, който определя формата на този пластир. Този начин за дефиниране на повърхност се нарича форма на тензорно произведение.
Ориз. 11.54. Пример за кръпка на Безие Като цяло контролният полиедър е мрежа от (M + 1)(I + 1) върхове и изразът за повърхността е:
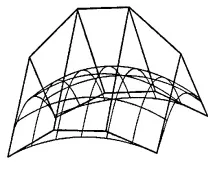
Създаване на криви и повърхности
За да формира пластир, дизайнерът внимателно задава позициите на тези върхове и след това, използвайки уравнение (11.91), определя формата на повърхността. Упражненията по-долу изследват алтернативна матрична форма на повърхност на Безие.
На фиг. 11.55 показва пример за бикубичен пластир на Безие (тук L = M = 3) и неговия контролен полиедър. За повече подробности относно кривите на Безие вижте [Rogers, 174].
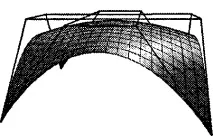
Ориз. 11.55. Бикубичен пластир на Безие и неговият контролен полиедър Практически упражнения
11.11.1. Възстановяване на междинна форма Как се конструира контролният полиедър, използван в уравнение (11.91), така че да има линейна интерполация между двата контролни многоъгълника?
11.11.1. Нормали към кръпки на Безие Като използвате параметричната форма на кръпка на Безие в уравнение (6.25), извлечете (комплексен) израз за нормалния вектор към тази кръпка. Опростете получения израз колкото е възможно повече. Нормалният вектор варира ли непрекъснато за всички стойности на (u, o)?
11.11.3. Алтернативна форма на пластир на Безие Следната форма на бикубична (7. - M - 3) повърхност на Безие ще помогне да се демонстрира съвместното поведение на нейните части "images/tmp8E4A-815.png" />
Външните двойки вектори и матрици създават полиноми на Бърнщайн, докато вътрешната матрица съдържа геометрията на пластира.
О Сравнете уравнение (11.92) с подобна форма на криви на Безие, дадени от уравнение (11.41).
Програмиране с OpenGL
Организацията на работното пространство е проблем, който е от значение за всеки офис или офис.
Ако преди десетина години можехте да гледате любимия си филм само по телевизията или в киното, днес индустрията за свободното време е много по-развита и вече няма нужда да следите телевизионната програма, достатъчно е да имате интернет
Кои са бизнесмени и къде да ги намерим
Съвети как да се справите с вирусите