Фундаментален набор от графични цикли
Да предположим, че трябва да използваме закона на Кирхоф, за да съставим система от линейни уравнения за електрическа верига. Веригата има сложна структура и съдържа голям брой цикли. Нека напишем закона на Кирхоф за всеки цикъл и да започнем да решаваме получената система от уравнения. Веднага се оказва, че някои от уравненията са линейно зависими, т.е. получени от други. Значи не са били необходими някакви цикли?!
В тази глава ще бъде доказано, че ВСЕКИ ЦИКЪЛ на графика може да бъде уникално разложен на ФУНДАМЕНТАЛНИ ЦИКЛИ на тази графика по същия начин, както всеки вектор на триизмерното пространство е уникално представен чрез линейна комбинация от базисни векториi,j,k. Ще бъде показано също как да се конструира този фундаментален набор за дадена графика.
По-нататък граф ще означава свързан неориентиран граф, а цикъл ЕЛЕМЕНТАРЕН ЦИКЪЛ.
Първо, за произволни множества A и B въвеждаме операцията за вземане на СИМЕТРИЧНАТА РАЗЛИКА A B=(A B)/(A B).
Нека построим симетричната разлика на три множества. Нека изберем реда на действията, съответстващ на следното разположение на скобите: (A B) C.
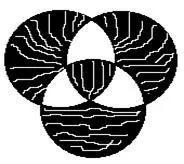
По силата на симетрията при всяко подреждане на скоби ще се получи едно и също множество A B C. Може да се установи закономерност: симетричната разлика включва елементи, съдържащи се едновременно в едно или три множества, а тези, които принадлежат на две, се премахват. Ние обобщаваме този резултат до произволен брой набори.
Симетричната разлика на множества A1, A2, ..., Ak съдържа точно онези елементи, които принадлежат на НЕЧЕТЕН брой множества.
Това може да се докаже чрез индукция върху броя на множествата.
Да се върнем към фундаменталните цикли. Този набор се определя чрез рамката на графиката.
Нека рамката D = на графа G= вече е изградена. Ако към рамкатадобавете произволен акорд e (E \ T), тогава получената графика (D e) ще съдържа точно един цикъл. Нека наречем този цикъл Ce.
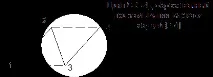
Добавяйки последователно всички акорди към рамката, получаваме ФУНДАМЕНТАЛЕН набор от цикли Ф по отношение на рамката D Ф = e : e (E\T)>.
?Въпрос 1. Посочете фундаменталното множество от цикли на графа G по отношение на рамката D на фигура 8.18.
Симетричната разлика на произволен брой цикли на графиката G е цикъл на графиката G.
?Въпрос 2. В графика G (фигура 8.18) намерете C1 C2, ако C1=(1-2-3), C2=(2-3-4).
Ние формулираме без доказателство.
Произволен цикъл C на графиката G може да бъде уникално представен като симетрична разлика на някакъв брой ФУНДАМЕНТАЛНИ ЦИКЛИ.
С други думи, всеки цикъл се разлага според основата на фундаменталните цикли.
Както вече беше споменато, познаването на фундаменталните цикли е от съществено значение при анализа на ЕЛЕКТРИЧЕСКИ ВЕРИГИ.
За всеки основен цикъл на тази верига може да се напише законът на Кирхоф: сумата от падовете на напрежението по цикъла е 0. Всички тези уравнения са независими, уравненията за останалите цикли ще следват от тях.
Ръбът (v-u), анализиран от алгоритъма, ще затвори цикъла, ако (v-u) е хорда.
КРИТЕРИЯТ ЗА АКОРД е както следва:
(v-u) ще бъде акорд, ако u - намереният съсед на v - вече е бил срещан преди при търсене в дълбочина. В този случай той е на СТЕК и неговият номерGLN(u) е по-малък от съответния номерGLN(v). Но това не е всичко. Ако от u стигнем до върха v, тоест u е бащата на v, тогаваGLN(u)
Данни: Графика G= , представена от RECORD[V], v V списъци.
Резултати: Множеството от фундаментални цикли Ф на графа G.
Променливите: d, num, STACK, RECORD, GLN са глобални.
1 процедура LOOP(v);
4num:=num+1; GLN[v]:=номер;
5 за u RECORD[v] do
6 ако GLN[u]=0 тогава LOOP(u)
7 else if (u<>STACK[d-1]) AND (GLN[u] се нарича АРТИКУЛ, ако премахването на този връх и всички ребра, излизащи от него, води до увеличаване на свързаните компоненти на графиката.
Ако един свързан (състоящ се от 1 свързан компонент) граф няма точки на артикулация, той е ДВОЙНОСВЪРЗАН.
Всеки МАКСИМАЛЕН двусвързан подграф на граф G се нарича ДВИКЪВЪРЗВАЩ КОМПОНЕНТ или БЛОК на този граф.
?Въпрос 1. Какво ще бъде пресечната точка на два различни графични блока?
?Въпрос 2. Какво се случва с блок, ако добавим към него ребро на графика, което има обща точка с блока и не принадлежи на блока?
Бисвързаността на графа е много полезно свойство за някои приложни проблеми.
Представете си, че върховете на графа са телеграфни станции; ребрата са предавателни линии. Да предположим, че една от станциите не работи. Ако графиката е двойно свързана, тогава ще има връзка между всеки две останали станции.
За много проблеми е важно да знаете блоковете на графиката. Например, можете да намерите всички елементарни цикли на графа G ОТДЕЛНО за всеки блок на графика G.
Намирането на артикулационни точки и графични блокове е класически проблем. Ще търсим точки на артикулация, като обикаляме всички върхове на графиката, използвайки метода за търсене в дълбочина. Ние не само ще обиколим върховете на графа, но и ще изградим неговата РАМКА.
Когато се конструира телена рамка чрез търсене в дълбочина, за два върха w и v, свързани с ребро, винаги се знае точно: или w е потомък на v, или обратното. Как да разпознаем артикулационната точка s, ако рамката D на графиката G вече е изградена?
Ето КРИТЕРИЯ ЗА СТАТИЯТА:
или е корен, който има поне двама сина в D;
или върхът s има поне един син u, така че нито той, нито неговите потомцисвързани с акорди с предците на s.

Разгледайте фигура 8.21. Номерата на върховете са числата, които върховете на графа получават по време на изграждането на телената рамка. Нека покажем, че върхът s удовлетворява второто условие на критерия.
Чрез конструкцията на рамката s има син: 3 и потомък 4. Предшественик на s е връх k. Син 3 и неговият потомък 4 не са свързани чрез акорди с k. И така, s е артикулационна точка и графиката G има блок 1=.
?Въпрос 3. С кой връх трябва да бъде свързан връх 4, за да може графът G да стане двусвързан?
Върхът k е артикулационна точка, тъй като е корен, който има две деца: s и 5. Следователно графът G има блок 2 = и блок 3 = .
Познавайки критерия за артикулационната точка, ще опишем АЛГОРИТЪМА за намиране на тези точки.
Нека алгоритъмът за първо търсене в дълбочина изгради рамка D на граф G. За всеки връх v ще изчислим две стойности:GLN[v] иMIN[v].
GLN[v] е просто число, което един връх получава при изграждане на телена рамка. Например за коренGLN[k]=1.
Нека върхът v е свързан чрез ХОРДИ (помнете какво представляват хордите за скелета D!) с някои върхове X1, …, Xk. Избираме минималния брой на тези върхове:
?Въпрос 4. Кои върхове на графиката на фигура 8.21 са свързани с хорди с върха s?
Нека w е произволен потомък на v. Може да се свърже и с хорди с някои върхове Y1, ..., Yp.
И накрая изчисляваме Y[w] за ВСЕКИ w - потомък на v и избираме най-малкия от тях.
Най-малкото от трите числа GLN[v], X[v], Y[v]> нека извикамеMIN[v]:
MIN[v] се изчислява лесно чрез индукция.
Нека за всички синове U1, …, Uk върховете vMIN[U1], …,MIN[Uk] вече са изчислени.
Да си припомним критериите. Точка на съчленяване е или корен с двама сина, или предците на тази точка и потомците на поне един син не сасвързани с акорди.
Ние записваме този критерий по отношение на GLN и MIN.
MIN[u] е минималният брой върхове, към които синът u и неговите потомци са свързани. Ако сред тези върхове няма предшественици на v, тогава критерият ще бъде изпълнен. Броят на предците е строго по-малък от GLN[v], така че MIN[u] ³ GLN [v] за някой син u на v.
?Въпрос 5. Изчислете MIN[3] за син 3 на s. Ще бъде ли изпълнен критерият за s?
Данни: Графика G = без изолирани върхове, представена от списъци с инциденти RECORD[v], v Î V.
Резултати: Наборът от ръбове на всички двусвързани компоненти. Променливите MIN, GLN, CTEK,numса глобални.
1 процедура BLOC(v,p);
3num:=num+1; GLN[v]:=номер;
5 за u Є RECORD[v] do
6 ако GLN[u]=0 тогава
8 STACK = GLN[v] тогава
стек последен до (v-u) включително - блок, свързващ u на всички негови наследници>
14 e p) и (GLN[u] 1) блокове, и алгоритъмът работи правилно за всеки граф, съдържащ блокове без върхове с нечетна степен, представени от списъците с инциденти RECORD[v], v н V.
Резултати: Цикъл на Ойлер, съхранен в EC стека.
2 СТЕК:=НИЛ; EC:=НИЛ;
3 k := произволен връх G;
8 ако RECORD[v]<>0 тогава изход от v>
10 u:= първи връх на WRITE[v];