Информатика - Бройни системи

Бройни системи

Нека се запознаем с видовете бройни системи. Научете как да преобразувате числа от една бройна система в друга.

Цели:Да запознае учениците с видовете бройни системи. Научете учениците как да преобразуват числа от една бройна система в друга.

Позиционни и непозиционни бройни системи.
Радикс.
Двоични, осмични и шестнадесетични кодове на числата.

обсъждат разнообразието от бройни системи;
покажете с примери превода на числа от произволна позиционна система в десетична;
обясняват алгоритъма за преобразуване на числата от десетичната система в други позиционни;
показват "афинитета" на двоичните, осмичните и шестнадесетичните системи и учат как да превеждат в тези бройни системи.

Тип урок: комбиниран.

Организационен момент. Тема, цели, задачи за урока.

Актуализиране на основни знания.

Фронтално проучване по предишните теми „Форми на представяне на информация“ и „Кодиране“

Как се измерва информацията?
Колко бита са необходими за кодиране на 16 цвята?
Какво е кодиране?
С един байт, колко различни комбинации от двоичен код могат да бъдат получени?

Телевизори - 3 човека

Нов материал.

Дефиницията на бройната система е набор от техники и правила за записване на числа с помощта на определен набор от знаци.

ДИАЛОГ

Въпрос: Каква бройна система се използва навсякъде в наше време? Отговор: Десетичен.
Въпрос: Колко цифри има в десетичната система? Отговор: десет
Въпрос: Какви са тези числа? Отговор: Числата от 0 до 9.
Въпрос: Променя ли се десетичното число,ако пренаредите числата в него? Отговор: Да, променя се.

За писане на числа могат да се използват не само цифри, но и букви. Едно и също число може да бъде представено по различен начин в различни бройни системи.

В зависимост от начина на представяне на числата бройните системи се делят на позиционни и непозиционни.

Внепозиционнатабройна система числата не променят своята количествена стойност при промяна на местоположението (позицията) им в числото. Пример за непозиционна система е римската система, в която, независимо от местоположението, един и същ знак има една и съща стойност(например знакът X в числото XXV),в която "тежестта" на числото не зависи от реда на знаците в числото.

(1 - I, 5 - V, 10 - X, 50 - L, 100 - C, 500 - D, 1000 - M).

В позиционнитебройни системи стойността на цифрата зависи от нейната позиция (място) в числото. Например числото 444 се записва с три еднакви цифри, но всяка от тях има свое значение: четири стотици, четири десетици и четири единици. Тоест, може да се напише така:

444 = 4. 100 + 4 . 10 + 4 . 1 или 444 = 4 . 10 2 + 4 . 10 1 + 4 . 100 .

Числото 10, чиито степени се използват в тази формула (а именно колко различни цифри има в десетичната система), се наричаоснована бройната система, а степените на десет сатеглацифри.

Значението на всяка цифра (нейното „тегло”) зависи от нейното място (позиция) при изписване на числото. Позицията (позицията) на цифра в числов запис определя нейния ранг; ако в числото няма цифра, тогава в записа на числото на нейно място се поставя числото 0. Знаем, че 10 единици от всяка цифра образуват нова единица от най-високата цифра. Числото 10 се нарича основа на десетичната бройна система. С негова помощопределя се “теглото” на единицата на всяка цифра.

Основата на позиционната бройна система определя броя на различните знаци, разрешени в бройната система.

Например числото 492 е трицифрено и в него 2 е цифрата на единиците, 9 е цифрата на десетиците, а 4 е цифрата на стотиците. В компютърната техника широко се използват двоичната, осмичната и шестнадесетичната бройна система.

двоична бройна система (p = 2), цифри 0 и 1.

октално(p=8), - 0, 1, 2. 7;

шестнадесетичен(p = 16), - O, 1, 2. 9 и букви - A, B, C, D, E, G, заместващи съответно числата 10, 11, 12, 13, 14, 15).

В общия случай всяко число N в позиционната бройна система може да бъде представено като:

N = ak*p k +ak-1*p k-1 +…+a1*p 1 +a0*p 0 +a-1*p -1 +…+a-n*p -n. Където ak е k-тата цифра от цялата част на числото N, записано в бройната система с основа p. a-n - n-та цифра от дробната част на числото N, записана с основа p. k+1 – броят на цифрите в цялата част на числото N. n – Броят на цифрите в дробната част на числото N.

С помощта на тази формула можете лесно да преобразувате число от бройна система с произволна основа в десетична.

Пример:325426= 3 . 6 4 +2 . 6 3 + 5 . 6 2 + 4 . 6 1 + 2 . 6 0 = 3 . 1296 + 2 . 216 + 5 . 36 + 4 . 6 + 2 = 3888 + 432 + 180 + 24 + 2 =4526

Решете на дъската:

517(8) =335(10) 10521(8) = 4433(10) 10011010(2) = 154(10).

Алгоритъм за преобразуване на цели числа от бройна система с основа p в бройна система с основа g.

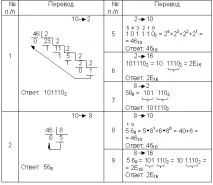
Последователно извършваме делението на даденото число и получените цяло числа на основата на новата система за деление, докато получим частно, по-малко от делителя.(Получените остатъци, които са цифри на число в новата бройна система).
Съставете число в новата бройна система, като го запишете, като започнете с последния остатък.

Преобразувайте десетично число N == 11 (p = 10) в двоична бройна система (p = 2).

2000 : 8 = 250 (рез. 0) 250 : 8 = 31 (рез. 2) 31 : 8 = 3 (рез. 7) 3 : 8 = 0 (рез. 3) 1011(2) = 11(10) 2000(10) = 3720(8)

23(10) = (2) 168 (10) = (8) 216 (8) = 10001110(2)

D/zконвертиране от десетичен в двоичен 231, 545; от двоично към десетично 1001, 11101.

Оценяване:Тестовете са получили оценки...

Ще проверя картите и ще ги публикувам в следващия урок.

Допълнително:

Умножението продължава, докато се получат нули в дробната част.

Отговор: 1001 0110.11.

Какви форми на представяне на информация познавате?
Колко бита съдържа думата "Компютър"? Оправдавам.
Колко бита съдържа черно-бяло изображение 100*100 точки? Оправдавам.

Карта

Какви форми на представяне на информация познавате?
Колко бита съдържа думата "Компютър"? Оправдавам.
Колко бита съдържа черно-бяло изображение 100*100 точки? Оправдавам.