Интерполация в цифровата осцилография

Дискретни измервания и проблемът за възстановяване на сигнала

Тъй като цифровите осцилоскопи, за разлика от техните аналогови аналогове, не измерват входния сигнал непрекъснато, а само в отделни моменти, възниква проблем при представянето на осцилограма на потребителя: от една страна, устройството трябва да показва резултатите от измерването възможно най-точно, от друга страна, е трудно визуално да се възприеме формата на сигнала, изобразен просто от набор от точки. По-долу има анимиран чертеж, изобразяващ осцилограма с отделни точки и непрекъсната линия [тези и всички следващи илюстрации в статията са получени с помощта на програматаAKTAKOMОсцилоскопPro версия 2.0.4.5 и осцилоскопACK-4106]. На практика е невъзможно да се долови определен сигнал в пунктираните орнаменти на първата рисунка. Така че необходимостта от цифров осцилоскоп, който да може да "начертае непрекъсната линия в отделни точки", дори не се оспорва, въпросът е: как да го направим?

Изображение на осцилограма с дискретни точки и непрекъсната линия

Линейна интерполация

Задачата за възстановяване на аналогов сигнал от неговите дискретни образци, от гледна точка на математиката, не е нищо повече от добре познат проблем за интерполация на непрекъсната функция F(x) чрез краен брой N от нейните точки X0, X1,… Xi,… XN. Тези точки, където е дадена стойността на функцията, се наричат интерполационни възли. Тъй като в общия случай природата на интерполираната функция не е известна предварително, проблемът с интерполацията обикновено се свежда до проблема с апроксимацията на части: необходимо е да се изберат прости аналитични функции, които ще се считат за приближения на оригиналната функция между възлите. В самите възли стойностите на апроксимиращите функции трябва да съответстват на дадените стойности на оригиналафункции. Най-простото решение би било приближение чрез линейни функции във формата fi(x)=a+b(x-Xi). Геометрично, такава интерполация е начупена линия, състояща се от прави сегменти, свързани във възлите:

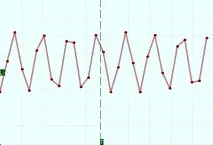
Интерполация чрез полиноми, задача за звънене

Ъгловият вид на линейната интерполация веднага подсказва, че това не е най-точното представяне на оригиналния сигнал. Наистина знаем, че честотната лента на измервателния път е ограничена. Спектърът на остроъгълната вълна, показана на фигурата по-горе, е безкраен. Следователно, по-точно представяне би било приближение чрез по-гладка функция.

Такова решение се дава например чрез метода на интерполация чрез кубични функции на части. Идеята на метода е, че първоначалната функция на всеки сегмент [Xi, Xi+1] се апроксимира с полином от трета степен (т.е. функция от формата fi(x)=a+b(x-Xi)+c(x-Xi) 2 +d(x-Xi) 3 ), докато не само стойностите на съседните полиноми съвпадат във възлите, но и техните първи производни (т.е. fi(X) i+1)=fi+1(Xi+1) и f'i(Xi+1)=f'i+1(Xi+1)). Стойностите на производните на интерполиращите полиноми се избират произволно въз основа на допълнителна информация за естеството на оригиналната функция. Ако няма допълнителна информация, обикновено разделените разлики се използват като стойности на производни: f’(Xi)=(F(Xi+1)-F(Xi))/(Xi+1-Xi).

Условието за непрекъснатост на производната гарантира плавността на резултантната форма на вълната, но причинява неприятен страничен ефект, наречен ефект на звънене.

Обърнете внимание на извънредните стойностипредипредната част и ръба. Ако вълнатаследна фронта все още може да се обясни с затихнали трептения, които възникват след рязка промяна в състоянието на сигнала, тогава трептенията, които се появяват предварително преди събитиетоса физически невъзможни.

Интерполация чрез кубични полиноми на Бесел

Всъщност това са фалшиви пикове и появата им на осцилограмата се дължи само на избрания характер на интерполиращата функция.

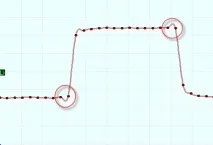
Използвайки произвола при определяне на стойностите на производните на интерполиращите полиноми, можете да опитате да сведете до минимум тези изкривявания. Например, методът на интерполация на Akima взема предвид, когато избира производна във възлите, гладкостта на оригиналната функция в областите, съседни на този възел. За да направите това, производната във всеки възел се приема за равна на средната стойност на разделената разлика от първи ред отдясно и отляво, а осредняването се извършва с тегла, съответстващи на модула на разделената разлика от втори ред от същата страна. Пример за интерполация на Акима е представен по-долу, той се изпълнява за същия набор от възлови точки като интерполацията на Бесел.

Сплайн интерполация Akima

Sinc интерполация (Sin(X)/X), ограничения на приложимостта, филтър Lanczos

Интерполация чрез частични кубични функции или сплайн интерполация, както често се нарича, работи добре в случаите, когато има граница в честотата на дискретизация, т.е. в случаите, когато броят на измервателните точки за период е достатъчно голям (десетки или повече). Но когато осцилоскопът работи в екстремни ситуации, когато честотата на измерения сигнал се доближава до честотата на Котелников, т.е. до половината от честотата на дискретизация, сплайновете дават напълно незадоволителен резултат. Фигура 6 показва пример за интерполация на 39 MHz синусоидална форма на вълната, взета при 100 MHz. Както можете да видите, сплайн интерполацията (сини и зелени линии) показва формата на вълната много далеч от оригиналния синус. Това е разбираемо: има малко точки на измерване и съответно малкоинформация за формата на вълната и няма начин да се познае, че между две точки близо до тригерната линия (пунктирана вертикална линия в центъра на фигурата) сигналът има пик с амплитуда, много по-голяма от най-близките опорни точки. Или има такъв начин?

Да, има такъв начин. Нека броят на точките за период е ограничен, но като вземем предвид допълнителни съображения, можем да възстановим формата на вълната. Да приемем, че спектърът на измерения сигнал е ограничен от честотата на Котелников. Наистина, ако това не е така, тогава условията за приложимост на уреда са нарушени и направените измервания са очевидно неверни и следователно не могат да бъдат обработени. След това, за да се конструира интерполационна крива, може да се използва формулата за интерполация Sin(X)/X, която е следствие от теоремата на Котелников:

Отбелязвайки, че в нашия случай разликата между възловите точки е постоянна и равна на периода на вземане на проби, както и използвайки традиционната нотация

можем да напишем синк-интерполационната формула в по-кратка форма:

Тъмночервената линия на фигурата е изградена с помощта на този тип интерполация и нейното предимство пред сплайн интерполацията в този случай е очевидно.

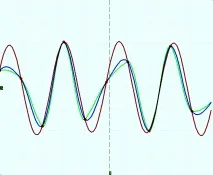
Интерполация при ниска честота на дискретизация. Честота на сигнала 39 MHz, честота на дискретизация 100 MHz. Синята линия е интерполация с полином на Бесел, зелената линия е интерполация на Акима, червената линия е интерполация на sinc

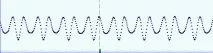
Интерполация с полином на Бесел, интерполация по метода на Акима, синк интерполация.

За съжаление този метод не е лишен от недостатъци. Първо, както може да се види от неговата основна формула, той изисква, за да изчисли всяка междинна точка, сумирането на безкрайна поредица от членове, които вземат предвид всички възможни дискретниизмервания на сигнала в миналото и бъдещето, което, разбира се, не е физически осъществимо. И второ, дори и да се ограничим до волевото решение само с точките, налични в осцилограма, изчислителната сложност на метода е много по -висока, отколкото при интерполация на шплината: ако броят на операциите за изчисляване на частично полити, както се разраства, както се разраства, както се разраства, тъй като се разраства, както и за това, че се разраства с дължината.

На практика както първият, така и вторият проблем обикновено се решават с помощта на прозоречни функции, които ограничават областта на изчисляване на интерполираната точка до някои малки квартали, а теглото на най-близките възлови точки е по-високо от далечните. Могат да бъдат избрани подходящи прозоречни функции като триъгълен прозорец или прозорец на Гаус. Програмата AKTAKOM Oscilloscope Pro използва за тази цел функцията прозорец Lanczos, която също се основава на използването на функцията sinc. Коефициентите на тази функция се изчисляват, както следва:

Тук параметърътrе "радиусът на филтъра", показващ размера на прозореца.

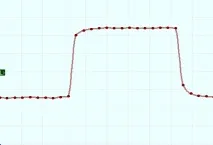
Третият недостатък на sinc интерполацията е продължение на нейното основно предимство - ограничения спектър на реконструирания сигнал. Вижте илюстрациите по-долу. Тук наблюдаваме 5 MHz правоъгълен сигнал, цифровизиран на 100 MHz. Това е максималната честота на дискретизация в реален режим за осцилоскопа ACK-4106, но това устройство има и строб режим, така че честотната му лента е по-висока от необходимите 50 MHz според Котелников и също е 100 MHz. В резултат на това интерполаторът sinc, прекъсвайки всички компоненти на спектъра над 50 MHz в осцилограмата, показва значителни изкривявания на сигнала на звънене (тъмночервена линия), които са особено забележими вв сравнение с интерполацията на Akima (зелена линия).

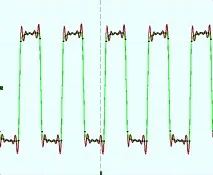
Интерполация на правоъгълен сигнал. Честота на сигнала 5 MHz, честота на дискретизация 100 MHz. Зелената линия е интерполация на Akima, червената линия е sinc интерполация

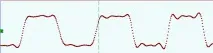
Фигурата показва спектрите на сигнала след интерполация на Akima и след интерполация sinc.

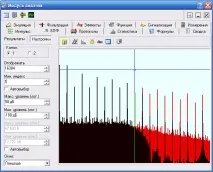
Спектър на интерполирани сигнали. Хоризонталният обхват на графиката е от 0 до 100 MHz. Курсорът маркира честотата от 50 MHz - половината от честотата на семплиране. Прозорецът на Lanczos беше използван за намаляване на хармоничното размазване. Червено показва спектъра на правоъгълен сигнал след интерполация по метода на Акима, черно показва спектъра на същия сигнал след sinc интерполация. Има рязък спад в честотната лента над честотата на Котелников.

Плюсове и минуси на различните видове интерполация. Автоматичен избор на метод

Нека да обобщим. Най-простият и бърз метод на интерполация е линейната интерполация, която просто свързва възловите точки с прави линии. При подробно разглеждане на формата на вълната качеството на картината е незадоволително, но в случаите, когато честотата на изследвания сигнал е ниска в сравнение с честотата на дискретизация, а броят на точките, показани на екрана, напротив, е сравним с неговата разделителна способност, използването на този метод е оправдано поради най-високата скорост на работа.

Сплайн интерполацията е малко по-бавна от линейната интерполация, но качеството на възпроизвеждане на сигнала е много по-високо. Използвайки различни методи за сплайн интерполация, като Bessel за по-плавно възстановяване на сигнала или Akima за минимизиране на фалшивите трептения, нискочестотните сигнали могат да бъдат възстановени бързо и ефективно.

И накрая, интерполацията sinc е най-добрият начин за реконструиране на високочестотни сигнали отминимални възлови точки. Той обаче е най-бавният от разглежданите (например на моя компютър, тъй като интерполацията на пълна форма на вълната от 64 000 точки в програмата AKTAKOM Oscilloscope Pro отне малко повече от три секунди, докато сплайн интерполацията на същата форма на вълната отне само 250 милисекунди). Освен това умишлено ограничава спектъра на възстановения сигнал, което може да доведе до силно звънене в сигнални участъци със стръмни фронтове.

Oscilloscope Pro позволява на потребителя самостоятелно да избере метода на интерполация, който счита за най-подходящ за неговите условия на измерване (или да изключи напълно интерполацията) и да каже на програмата автоматично да избере метода в зависимост от параметрите на сигнала.