Изграждане на приблизителни размахи на неметенеповърхности - Studiopedia
Общата техника за конструиране на приблизителни разработки на такива повърхности е следната:
1. Тази повърхност е разделена на равни или приблизително равни части.
2. Всяка такава част се апроксимира (заменя) с разгъната повърхност.
3. Построена е разработка на тези части, чиято съвкупност е приблизителна разработка на неразвиваща се повърхност. На колкото повече части е разделена кривата повърхност, толкова по-близка по форма апроксимиращите повърхности ще възпроизвеждат дадената.
Приблизителните развития на повърхности на въртене с криволинейни образуващи обикновено се изграждат по метода на спомагателни цилиндри или конуси, които са описани или вписани в дадена повърхност.
Пример 6. Постройте разработка на сферична повърхност (фиг. 12.7).
Решение. При изграждането на развитие на сфера, като всяка повърхност на въртене с криволинейна генератора, повърхността се разделя на тесни участъци с помощта на меридионални участъци. Всеки такъв дял ("венчелистче") се заменя с описаната цилиндрична повърхност, чиято ос минава през центъра на сферата (радиусът на цилиндричната повърхност е равен на радиуса на сферичната). В този случай цилиндричната повърхност се допира до тази сферична повърхност в точките на средния меридиан на лоба. Този среден меридиан е нормален участък от цилиндричната повърхност. Границите на цилиндричната повърхност на дяла ще бъдат меридианите, които го ограничават.
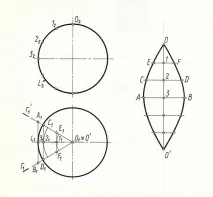
В нашия пример сферичната повърхност е разделена на 6 равни части. За да се получи по-точно развитие на сферична повърхност, тя се разделя на 12 или повече части. Помислете за конструкцията на приблизителен размах на едно "венчелистче", в което средният меридиане началният меридианl(l1, l2). Нека заменим това "венчелистче" с участък от цилиндрична повърхност, описана близо до него. Тази повърхност е фронтално проектирана и следователно генераторите се проектират върху проекционната равнина P1 в пълен размер. Нормалното сечение на цилиндричната повърхност на тази част е половината от главния меридианl(l1, l2), а границите на повърхността са равнините на ограничаващите я меридиани ГГ' (Г1Г1').
За да изградим разработка на тази цилиндрична повърхнина, я заместваме с вписана призматична повърхнина, за което разделяме половината от главния меридиан (l) на 6 равни части и прекарваме образуващите AB (A1B1), CD (C1D1), EF (E1F1) на цилиндричната повърхнина през разделителните точки 1(11), 2(21), 3(31).
Ние изграждаме разработката по метода на нормалното сечение. И тъй като нормалното напречно сечение на апроксимиращата повърхност е полуметридианътl, ние го скриваме в сегмента на OO '(01 = 0212) и през точките на деление 1, 2, 3, начертаваме перпендикуляр към него, върху който отбелязваме точки A, C, D, E, F, ..., като използваме съответните сегменти: AB = A1V1, CD = C1D1 и T. D . Свързвайки краищата на тези генератори с гладки криви, получаваме приблизително сканиране на 1/6 от сферата. Пълното почистване ще се състои от шест такива акции.
Същност на метода и основни понятия. Стандартни аксонометрични проекции. Правоъгълна изометрия. Правоъгълен размер. Наклонени аксонометрични проекции. Построяване на аксонометрични изображения върху ортогонални проекции. Точкова аксонометрия. Аксонометрия на равнинна фигура. Аксонометрия на призматична повърхност. Решение на позиционни задачи в аксонометрията.
Не намерихте това, което търсихте? Използвайте търсачката: