Изследване на функции и построяване на техните графики

Нека разделим процеса на изследване на функция на три етапа:

Напървия етапразгледайте аналитичния израз, който дефинира функцията:

и дефинирайте следните характеристики.

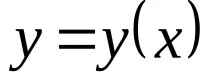
Това са стойностите на независимата променливаx, за която съществува функцията. Въпросът за определяне на диапазона от приемливи стойности се разглежда подробно в хода на средното училище.

Нули на функцията и точки на пресичане с оста OY

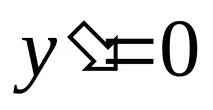
Нулите на функцията са точките, къдетоy= 0 (пресечни точки с оста OX) Тези точки разделят интервалите, в които функцията запазва знака си. Получените точки помагат за изграждането на графика.

странно, общо

Графикана четнафункция:

е симетрична спрямо оста OY.

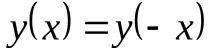
Начертайтенечетнафункция:

симетрична по отношение на началото.

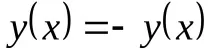
Изследване на точки на прекъсване и поведение на функцията на границите на ODZ

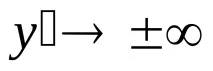
Вижте тема 4, класификация на точките на прекъсване.Вертикалните асимптотина функцията са разположени в точките на прекъсване от втори род.

Теорема.За да бъде правата

асимптотана функция, е необходимо и достатъчно да има крайни граници:u.

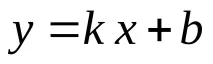
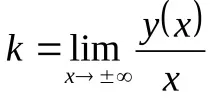
 Лимитите се изчисляват отделно за

и. Следователно максималният брой асимптоти е две. Ако поне една граница е безкрайна или не съществува, няма съответстваща асимптота.

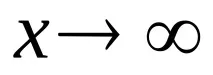
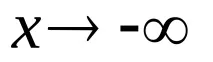
Навтория етапнамираме първата производна на функцията и чрез нейния аналитичен израз определяме следните характеристики на самата функция.

Точки на възможни екстремуми −критични точки

Това са точки, в които

(стационарно), или, илине съществува. Критичните точки и точките на прекъсване разделят интервалите на монотонност на функцията.

Интервали на увеличение / намаляване (монотонност). Обозначения:  - увеличава, - намаляваща

Теорема.За да бъде непрекъсната функция с непрекъсната производнамонотоннана някакъв интервал

, е необходимо и достатъчно нейната първа производна да запази знака си на този интервал.

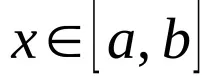
, или на

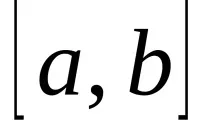
Крайности (макс./мин.)

Теорема 1.За да може всякакритичнаточка да има екстремум, е необходимо и достатъчно първата производна на функцията да промени знака при преминаване през тази точка.

Теорема 2.За да съществува екстремум встационарнаточка, е необходимо и достатъчно втората производна на функцията да запази знака си в тази точка.

Г

графична илюстрация на теорема 1 за екстремума на функция.

Натретия етапще намерим втората производна на функцията и чрез нейния аналитичен израз ще определим следните характеристики на самата функция.

Това са точките, където

илиилине съществува. Точките на инфлексия разделят интервалите на изпъкналост/вдлъбнатост на функцията.

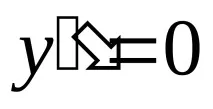
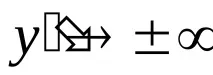
Интервали на изпъкналост / вдлъбнатост. Обозначения:  - вдлъбнат,  - изпъкнал

Теорема.За да бъде непрекъсната, два пъти диференцируема функция изпъкнала / вдлъбната / на някакъв интервал

, е необходимо и достатъчно нейната втора производна да запази знака си на този интервал.

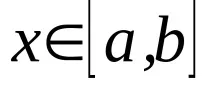
, или .

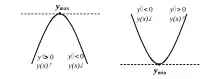
Графична илюстрация на теоремата за изпъкналост/вдлъбнатост на функция и теорема 2 за екстремума на функция.

P

Примерна схема за изучаване на функция и начертаване на нейната графика е дадена в разделПримери за изпълнение на задължителна домашна работа по тема 5.

---