KNOW INTUIT, Лекция, Физически модели на бази данни
Файлове със свободен индекс или файлове с последователен индекс
Нека се опитаме да подобрим начина, по който се съхранява файлът: ще го съхраним в подредена форма и ще приложим алгоритъм за двоично търсене за достъп до произволен запис. Тогава времето за достъп до произволен запис ще бъде значително по-малко. За нашия пример това би било:
T = log2KBO = log212500 = 14 дискови достъпа.
А това е значително по-малко от 12 500 достъпа за произволно съхранение на файлови записи. Въпреки това поддържането на основния файл по редовен начин също е сложна операция.
Създаден е свободен индекс специално за подредени файлове. За тези файлове се използва принципът на вътрешно подреждане, за да се намали броят на съхранените индекси. Структурата на записа в индекса за такива файлове е както следва:
В областта на индекса сега търсим желания блок по зададената стойност на първичния ключ. Тъй като всички записи са подредени, стойността на първия запис на блока ни позволява бързо да определим в кой блок се намира желаният запис. Всички други действия се извършват в основната зона. На фиг. Фигура 9.8 показва пример за това как да попълните основните и индексните области, ако първичният ключ е цели числа.
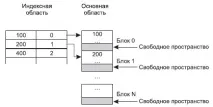
Времето, необходимо за сортиране на големи файлове, е значително, но тъй като файловете се съхраняват сортирани от момента, в който са създадени, разходите за добавяне на нова информация ще бъдат много по-малко.
Нека оценим времето за достъп до произволен запис за файлове с разхлабен индекс. Алгоритъмът за решаване на проблема е подобен.
LI = LK + 2 = 14 + 2 = 14 байта.
Тогава броят на индексните записи в един блок ще бъде равен на:
КИЗБ=LB/LI = 1024/14 = 73 индексни записа в един блок.
Определете броя на индексните блокове, необходими за съхраняване на необходимите индексни записи:
KIB = KBO/KZIB = 12500/73 = 172 блока.
Тогава ще се определи времето за достъп по предходната формула:
Tsearch = log2KIB + 1 = log2172 + 1 = 8 + 1 = 9 дискови достъпа.
Виждаме, че при преминаване към свободен индекс времето за достъп намалява почти един път и половина. Следователно може да се признае, че организирането на свободен индекс дава печалба в скоростта на достъп.
Обмислете процедурите за добавяне и изтриване на нов запис с подобен индекс.
Тук механизмът за включване на нов запис е коренно различен от разгледания по-рано. Тук трябва незабавно да се въведе нов запис в необходимия блок на необходимото място, което се определя от зададения принцип на подреждане върху набора от стойности на първичен ключ. Следователно първо се търси необходимия блок от основната памет, в който трябва да се постави нов запис, след което този блок се чете, след което съдържанието на блока се коригира в RAM и отново се записва на диска на старото място. Тук, както и в първия случай, трябва да се зададе процентът на първоначално запълване на блока, но само по отношение на основната площ. В MS SQL сървъра този процент се нарича Full-factor и се използва при формиране на клъстерни индекси. Клъстерираните са просто индекси, в които оригиналните записи са физически подредени по стойностите на първичния ключ. Когато се направи нов запис, областта на индекса не се коригира.
Броят достъпи до диска за добавяне на нов запис е равен на броя достъпи до диска, необходими за намиране на съответния блок, плюс един достъп, необходим за запис на модифицирания блокстаро място.
Tadd = log2N +1 + 1 попадения.
Унищожаването на запис става чрез физическото му премахване от основната област, а индексната област обикновено не се актуализира, дори ако първият запис на блока е изтрит. Следователно броят на достъпите до диска при изтриване на запис е същият като при добавяне на нов запис.
Организация на индексите под формата на B-дърво (B-дървета)
Терминът калк "B-tree", който смесва английския знак "B" и допълнителна дума на български, е толкова утвърден в литературата за организацията на физическото съхранение на данни, че няма да се осмеля да го коригирам.
След като по някакъв начин срещнах термина "B-дърво", аз го тълкувах дълго време, защото вече бях свикнал с установеното обозначение. Затова ще работим с този термин.
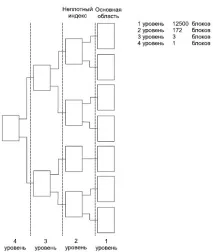
Изграждането на B-дървета е свързано с простата идея за изграждане на индекс върху вече изграден индекс. Наистина, ако изградим свободен индекс, тогава самата област на индекса може да се разглежда от нас като основен файл, върху който трябва да изградим отново свободен индекс, след което изграждаме следващия отново върху новия индекс и така нататък, докато остане само един индексен блок.
В общия случай ще получим дърво, на което всеки родителски блок е свързан с еднакъв брой подчинени блокове, чийто брой е равен на броя на индексните записи, поставени в един блок. Броят на достъпите до диска за търсене на всеки запис е еднакъв и равен на броя на нивата в конструираното дърво. Такива дървета се наричат балансирани (уравновесени) именно защото пътят от корена до всяко листо в това дърво е един и същ. Терминът "балансиран" от английския "balanced" - "балансиран, балансиран" даде името на този метод на организацияиндекс.
Нека да изградим подобно дърво за нашия пример и да изчислим броя на нивата за него и съответно броя на достъпите до диска.
На първо ниво броят на блоковете е равен на броя на блоковете в основната зона, знаем това - той е равен на 12 500 блока. Второто ниво се формира от свободен индекс, ние също го изградихме и изчислихме, че броят на блоковете в областта на индекса в този случай е 172 блока. Сега нека изградим свободен индекс върху това второ ниво отново.
Няма да променим дължината на индексния запис, но ще го считаме за същия, равен на 14 байта. Знаем също броя на индексните записи в един блок и той е равен на 73. Следователно веднага определяме колко блока трябва да съхраняваме връзки към 172 блока.
KIB3 = KIB2/KZIB = 172/73 = 3 блока
Отново закръгляме нагоре, защото последният, трети, блок няма да бъде напълно запълнен.
И ние изграждаме нов над третото ниво и на него ще има само един блок, в който ще има само три входа. Следователно броят на нивата в конструираното дърво е четири и съответно броят на достъпите до диска за произволен достъп за запис е четири (фиг. 9.9). Това не е максималният възможен брой достъпи, но винаги един и същ, еднакъв за достъп до всеки запис.
Механизмът за добавяне и изтриване на запис при организиране на индекс на B-дърво е подобен на механизма, използван в случай на разреден индекс.
И накрая, последното нещо, което бих искал да изясня, е съществуването на втори имена за плътни и неплътни индекси.
При плътен индекс, след намиране на местоположението на желания запис, достъпът до него се осъществява по директен начин по номера на записа, така че този начин на организиране на индекса се нарича index-direct.