Концепцията за правилни многостени

Многостенът еправилен, ако всичките му лица са еднакви правилнимногоъгълници и всички многостенни ъгли са еднакви (например куб).

От тази формулировка получаваме, че вправилните многостени всички равнинни ъгли, всички двустенни ъгли и всички ръбове са еднакви.

За да уточним коиправилни многоъгълници могат да действат като лица направилни многостени, вземаме предвид, че в полиедърен ъгъл най-малкият брой лица е три и че сумата от всички равнинни ъгли е по-малка от 4d (d = 90 0 )

Всеки ъгълна правилен триъгълник е равен на 2/3 d. Ако повторим 2/3 d членове 3 пъти, 4 пъти и 5 пъти, тогава резултатът ще бъде сбор по-малък от 4d. И ако повторим 2/3 d с термини 6 или повече пъти, тогава в резултат получаваме сума от 4d или повече. Поради тази причина отплоски ъгли, равни на ъглите на правилен триъгълник, е възможно да се образуватмногостенни ъгли само от три вида: тристенен, четиристенен и петстенен.

Ъгълътна квадрат е d, а ъгълътна правилен петоъгълник е 6/5 d. Повтаряйки тези ъгли с членове 3 пъти, в резултат получаваме суми, по-малки от 4d, и повтаряйки 4 пъти или повече, имаме 4d и повече. Поради тази причина от плоски ъгли, равни на ъглите на квадрат или правилен петоъгълник, могат да се образуват самотристенни ъгли.

Ъгълътна правилен шестоъгълник е 4/3 d. Съответно от такива ъгли не може да се образува дори тристенен ъгъл. От ъглитена правилни многоъгълници, имащи повече от 6 страни, още повече, че няма да е възможно да се образува един полиедърен ъгъл.

От горното можем да заключим, чеправилни многостени има само пет:

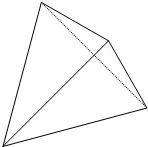
1.Правилен тетраедър (илитетраедър ), чиято повърхност е образувана от 4 правилни триъгълника.

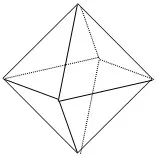
2.Правилен октаедър (илиoctaedron ), чиято повърхност е образувана от 8 правилни триъгълника.

3.Правилен двадесетстранник (илиикозаедър ), образуван от 20 правилни триъгълника.

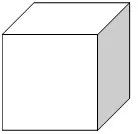
4.Правилен хексаедър (илиекзаедър ), образуван от 6 квадрата.

5.Правилен додекаедър (илидодекаедър ), образуван от 12 правилни петоъгълника.