Нови елементарни функции (имена, уравнения, графики) линейни, дробни линейни, степенни,

Пропорционалнистойности.Ако променливите y и x са правопропорционални, тогава функционалната връзка между тях се изразява с уравнението:

където k е константа (коефициент на пропорционалност).

Графиката на пряката пропорционалност е права линия, минаваща през началото на координатите и сключваща ъгъл с оста X, чийто тангенс е равен на k: tan =k (фиг.8). Следователно коефициентът на пропорционалност се нарича още фактор на наклона. Фигура 8 показва три графики за k = 1/3, k = 1 и k = -3.

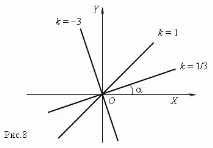
Линейна функция.Ако променливите y и x са свързани с уравнение от първа степен:

където поне едно от числата A или B не е равно на нула, тогава графиката на тази функционална зависимост е права линия. Ако C = 0, то преминава през началото, в противен случай не. Графики на линейни функции за различни комбинации от A, B, C са показани на фиг.9.

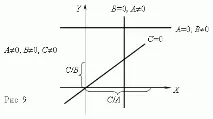
Обратна пропорционалност.Ако променливите y и x са обратно пропорционални, тогава функционалната връзка между тях се изразява с уравнението:

където k е постоянна стойност.

Графиката на обратната пропорционалност е хипербола (фиг. 10). Тази крива има два клона. Хиперболите се получават чрез пресичане на кръгъл конус с равнина (за конични сечения вижтераздел "Конус" в глава "Стереометрия"). Както е показано на фиг. 10, произведението на координатите на точките на хиперболата е постоянна стойност, в нашия пример равна на 1. В общия случай тази стойност е равна на k, което следва от уравнението на хиперболата: xy= k.

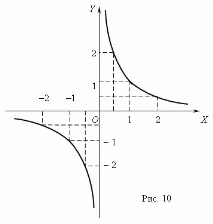
Основните характеристики и свойства на хипербола:

- област на дефиниране на функция: x 0, диапазон от стойности: y 0 ;

- функцията е монотонна (намаляваща) при x 0, но не

- неограничена функция, прекъсната в точката x = 0,нечетен, непериодичен;

Функцията няма нули.

4.

Квадратна функция.Това е функция:y=ax2 +bx+c, къдетоa, b, cса константи,a0. В най-простия случай:b=c<1 1> = 0 иy=ax2 . Графиката на тази функцияквадратна парабола -крива, минаваща през началото (фиг.11). Всяка парабола има ос на симетрияOY, която се наричаос на парабола. ТочкатаOна пресечната точка на параболата с нейната ос се наричавърхът на параболата.

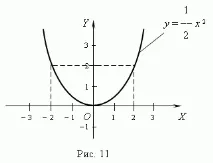
Графиката на функциятаy=ax2 +bx+cсъщо е квадратна парабола от същия тип катоy=ax2 , но върхът й не е в началото, а в точката с координати:

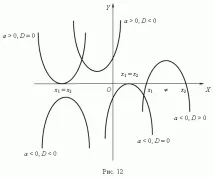
Формата и местоположението на квадратната парабола в координатната система изцяло зависи от два параметъра: коефициентaприx2 идискриминант D = b2–4ac. Тези свойства следват от анализа на корените на квадратното уравнение (вижтесъответния раздел в глава "Алгебра"). Всички възможни различни случаи за квадратна парабола са показани на фиг.12.

Степенна функция.Това е функция:y = axn, къдетоa, nса константи. Сn= 1 получавамепряка пропорционалност:y=ax; сn= 2 -квадратна парабола; сn= -1 -обратна пропорционалностилихипербола. По този начин тези функции са специални случаи на степенната функция. Знаем, че нулевата степен на всяко ненулево число е равна на 1, следователно приn= 0 степенната функция става постоянна стойност:y=a, т.е. нейният график еправа линия, успоредна на остаХ, с изключение на началото (моля, обяснете защо?). Всички тези случаи (заa= 1) са показани на Фиг.13 (n0) и Фиг.14 (n3 се наричакубична парабола.

Фигура 16 показва функцията. Тази функция е обратна на квадратната параболаy=x2 , нейната графика се получава чрез завъртане на квадратната парабола около ъглополовящата на първия координатен ъгъл. Това е начин да получите графиката на всяка обратна функция от графиката на нейната оригинална функция. Можем да видим от графиката, че това е двузначна функция (това също е обозначено със знака ± пред квадратния корен). Такива функции не се изучават в елементарната математика, следователно като функция обикновено разглеждаме един от нейните клонове: горен или долен.

Експоненциална функция.Функциятаy=ax, къдетоaе положително постоянно число, се наричаекспоненциална функция. Аргументxприемавсякакви валидни стойности;само положителни числасе считат за функционални стойности, тъй като в противен случай имаме многозначна функция. Така функциятаy= 81xима четири различни стойности заx= 1/4:y= 3,y= -3,y= 3iиy= -3i(моля, проверете! ). Но ние разглеждаме като стойност на функцията самоy= 3. Графиките на експоненциалната функция заa= 2 иa= 1/2 са показани на фиг.17. Те преминават през точката ( 0, 1 ). Сa= 1 имаме графика на права линия, успоредна на остаX, т.е. функцията става постоянна стойност от 1. Заa> 1 експоненциална функция нараства, a при 0 0 ;

Калкулатор

Обслужванебезплатна оценка на цената на работата

1. Попълнете заявление. Експертите ще изчислят цената на вашата работа
2. Изчисляването на цената ще дойде по пощата и SMS

Номерът на вашето приложение

Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.

---