Криви от втори ред
1. Конструирайте елипса, като зададете произволни стойности на голямата и малката ос. Намерете позицията на фокусите на елипсата.
2. Дефинирайте системата за параметризиране. Пребройте броя на параметрите на формата за елипса.
1. Конструирайте парабола, като зададете произволна стойност на фокусното разстояние.
2. Дефинирайте системата за параметризиране. Пребройте броя на параметрите на формата за парабола.
1. Конструирайте хипербола, като зададете произволни стойности на фокусното разстояние и разстоянието между върховете.
2. Дефинирайте системата за параметризиране. Пребройте броя на параметрите на формата за хипербола.
ИНФОРМАЦИЯ ОТ ТЕОРИЯТА
Елипса е плоска затворена крива, в която сумата от разстоянията на всяка нейна точка M до две дадени точки F 1 и F 2 е постоянна стойност и равна на голямата ос на елипсата:
M F 1 + M F 2 \u003d AB.
Осите на елипсата - голяма (BOE) AB и малка (MOE) CD - са взаимно перпендикулярни и едната разделя другата наполовина.
Ако от краищата на малката ос CD, като от центрове, опишете дъга от окръжност с радиус, равен на половината от голямата ос на елипсата R = OA = OB, тогава тя ще я пресича в точки F 1 и F 2, наречени фокуси (фиг. 9).
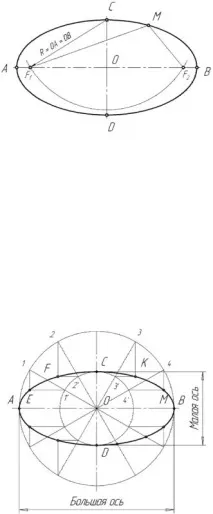
Фиг.9 Фиг.10 показва един от начините за построяване на елипса според нейния
брадви. Върху дадените оси AB и CD, както по диаметри, са построени две концентрични окръжности с център в точка O. Голям кръг е разделен на произволен брой части и получените точки са свързани с прави линии с центъра O. От пресечните точки 1 , 1 ′ , 2 , 2 ′ , 3 , 3 ′ , 4 , 4 ′ със спомагателни окръжности се изчертават отсечки от вертикални и хоризонтални линии до пресичането им в точките E , F , K , M принадлежащи на елипсата.
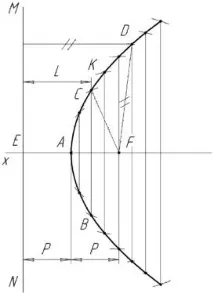
Параболата е плоска отворена крива линия, всяка точка от която е разположена нана същото разстояние от дадената права MN - директрисата, перпендикулярна на оста на параболата, и от фокуса F . Върхът на параболата А се намира в средата между фокуса и директрисата. Разстоянието от върха до фокуса (или от върха до директрисата) се нарича фокусно разстояние (p).
За да се построи парабола според дадена директриса и фокус, оста x на параболата се прекарва през точката F, перпендикулярна на директрисата MN. Отсечката EF се разделя наполовина и се получава върха А на параболата. Правите линии се изчертават перпендикулярно на оста на параболата на произволно разстояние от върха. От точка F с радиус, равен на разстоянието L от директрисата до съответната права линия, например SV, се правят прорези на тази права линия - точки C и B. След като по този начин са конструирани няколко двойки симетрични точки, през тях се изчертава гладка крива с помощта на шаблон (фиг. 11).

Хиперболата е плоска крива, в която разликата в разстоянията от всяка нейна точка до две дадени точки F 1 и F 2, наречени фокуси, е постоянна величина и е равна на разстоянието между нейните върхове A и B, например PF 1 - P F 2 = AB.
Хиперболата има две оси на симетрия - реална ab и имагинерна cd (фиг. 12). Две прави KL и K 1 L 1, минаващи през центъра 0 на хиперболата и докосващи нейните клонове в безкрайност, се наричат асимптоти.
Може да се построи хипербола от дадени върхове A и B и фокуси F 1 и F 2 . Върховете на хиперболата се определят чрез вписване на правоъгълник в окръжност, построена на фокусното разстояние (сегмент F 1 F 2 ), както на диаметъра. Произволни точки 1, 2, 3, 4 са маркирани на реалната ос ab вдясно от фокуса F 2 ... От фокусите F 1 и F 2 първо се изчертават дъги от кръгове с радиус, равен на разстоянието от