ЛЕКЦИЯ 16 Модели на изместване на несмесващи се течности
Най-развитата теория е едномерното движение на двуфазен флуид в пореста среда. Основните й предположения:
течностите се приемат за несмесими (взаимно неразтворими;
течностите се считат за несвиваеми, а порестата среда се счита за недеформируема; няма фазови преходи; фазовите вискозитетни коефициенти са постоянни;
относителните фазови пропускливости и капилярното налягане са известни недвусмислени функции на насищане;
хистерезисните явления не се вземат предвид (разглеждат се само еднопосочни процеси).
Въз основа на тези предположения е изведена пълна система от уравнения за двуфазна филтрация в хомогенна пореста среда, като се вземат предвид капилярните и гравитационните сили.
В случай на праволинеен паралелен поток по остаx(Фигура 16.1), уравненията за непрекъснатост (15.9) за фазите имат формата:
, . (16.1)
Обобщеният закон на Дарси (15.10) се свежда до уравненията:
, (16.2)
. (16.3)
Тукa –е ъгълът на наклона на остаxспрямо хоризонта (Фигура 16.1);r1 иr2 са фазови плътности.
Неизвестните характеристики на потокаs, u1, u2, p1и p2 зависят от координатата и времето.
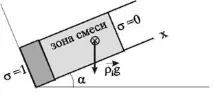
Фигура 16.1 - Схема на едномерна двуфазна филтрация, като се вземе предвид гравитацията
Уравнения (16.1), (16.2) и (16.3), като се вземе предвид (15.11), образуват затворена система за случаи на линеен поток, която е в основата на решаването на проблемите на изместване на една течност от друга. Характерна особеност на тази система е, че тя може да бъде сведена до едно уравнение за насищане. Познаването на разпределението на насищането в резервоара позволява да се анализира ефективността на изместване на нефт или газ от несмесваща се течност.
Това уравнение е сложнонелинейно уравнение от параболичен тип от втори ред. Точното решение на това уравнение е получено само за някои сравнително прости специални случаи. Получават се инвариантни решения (от типа на вълна, движеща се с постоянна скорост и самоподобни), както и някои числени решения на компютри.
При решаване на конкретни задачи за уравнението на изменение на насищането трябва да се формулират съответните гранични и начални условия. Като начално условие са дадени стойностите на неизвестната функцияsв зависимост от пространствените координати приt =0. Можем да приемем, че приt =0 наситеността е постоянна навсякъде (напримерs = s*).
В случай на изместване на нефт с вода, естествено е на входа на пласта (нагнетателен кладенец или галерия) дебитът на инжектираната вода и скоростта на филтриране на нефта да бъдат равни на нула. От последното условие в съответствие с формула (6.3) следва, чеk2=0, следователно, на тази повърхностs = s*.
На изхода от резервоара са възможни два варианта на гранични условия.
1. Можем да пренебрегнем градиента на капилярното налягане в сравнение с градиента на налягане във фазите, т.е. да приемем, че приx = L, от което следва, че:
приx = L. (16.4)
2. Експериментално е установено, че водата не изтича от хидрофилната формация, а се натрупва в изходния участък, докато насищането й достигнеs*. В момента, в който се достигне стойносттаs*, водата излиза от резервоара, като поддържа тази стойност на насищане на изхода. Това явление се нарича краен ефект. Математически той се свежда до сложно нелинейно гранично условие на изхода.
Нека се спрем на двата най-изследвани модела на двуфазна филтрация.
Модел Бъкли- Leverett. Без да се вземат предвид капилярните сили, двуфазната филтрация за случая на праволинейно-успоредно изместване е разгледана от S. Buckley и M. Leverett през 1942 г., а по-късно, независимо от тях, от A. M. Pirverdyan, който също изучава случая на по-общ закон за филтриране в двуфазен поток.
Уравнението на насищане за задачи от този тип принадлежи към класа на квазилинейните хиперболични уравнения от първи ред, които обикновено се решават по метода на характеристиките и имат свои собствени съществени характеристики в сравнение с параболичните уравнения.
В случай на едномерно (праволинейно-паралелно и равнинно-радиално) течение на несвиваеми несмесващи се течности при условия, при които капилярното налягане и ефектът на гравитацията могат да бъдат пренебрегнати, процесът на изместване е изучен доста пълно.
В разглеждания случай е важна така наречената функция на Бъкли-Леверет (Фигура 16.2) или функцията на разпределение на фазовия потокf(s),, която има просто физическо значение. Тя представлява съотношението на скоростта на филтриране на изместващата фаза към общата скорост и е равна на обемната част на потока на изместващата течност (вода) в общия поток на двете фази. По този начин функцията на Бъкли - Лаверет определя пълнотата на изместването и характера на разпределението на наситеността с нефт и газ в резервоара.
Задачите за увеличаване на добива на нефт и газов кондензат до голяма степен се свеждат до използването на такива действия върху формацията, които в крайна сметка променят формата на функциятаf(s) в посока на увеличаване на пълнотата на изместване.
Формата на кривите на функциятаf(s)и нейната производна е показана на фигура 16.2. С увеличаване на наситеносттаf(s) монотонно нараства от 0 до 1. Характерна особеност на графикатаf(s) е наличието на инфлексна точканаситеностsп,, както и области на вдлъбнатост и изпъкналост, където втората производна на//(s), съответно, е по-голяма и по-малка от нула. Тази особеност до голяма степен определя спецификата на задачите за изместваща филтрация в рамките на модела на Бъкли-Леверет.
Зависимостта на функцииf(s) и нейната производна от съотношението на фазовите вискозитети (вода и масло)m0=m1/ m2 е показано на Фигура 16.3. От тази фигура следва, че с увеличаване на съотношението на вискозитетите, криватаf(s) се измества надясно и ефективността на изместване се увеличава. Например, използването на пяна и сгъстители, които повишават вискозитета на инжектираната вода, може значително да увеличи добива на нефт.
Физическата характеристика на двуфазния модел на изместване на Buckley-Leverett е зависимостта на скоростта на разпространение на една или друга стойност на насищане от големината на това насищане (вълнова дисперсия). За 0£s £spголеми насищания се разпространяват с високи скорости, а заsp