Малко за минималните разстояния

Коварни стрели

Един типичен посетител на codeforces.com вероятно знае как да намери минимално (или дори максимално) обхващащо дърво (или дори обхващаща гора). Може да напише алгоритъм на Prim, алгоритъм на Kruskal. Някои може дори да са наясно, че всичко това са специални случаи на алгоритъма Boruvka, който през 1926 г. каза как да се електрифицира оптимално Моравия (регион на Чешката република). Но тези алгоритми работят правилно само за неориентирани графики.

Напомни ми за задачата. Дадена е претеглена графаG = (V, E, γ) (V е набор от върхове,E е набор от ръбове или дъги,γ е тегловна функция на ръбове или дъги). Изисква се да се намери подмножество от ръбове (дъги)S ⊆ E така че:

В графа(V, S) няма да има цикли (в ориентирания случай има допълнително ограничение: всеки връх трябва да съдържа не повече от една дъга отS ).
Сред тях, максимумът по отношение на включването: не можете да добавите друг ръб (дъга), така че предишното ограничение да не се счупи. Отбелязвам, че това предполага глобален максимум по отношение на броя на ръбовете (дъги).
Сред тях минималното тегло:γ(S) = γ(e) трябва да бъде сведено до минимум.

В неориентирана графа беше достатъчно (алгоритъмът на Крускал) да се вземат ребра по ред на нарастване на теглото, да се добавят към графиката, ако не образуват цикъл, или да се изхвърлят в противен случай. За съжаление, в случай на насочен график ни очаква неприятна изненада.

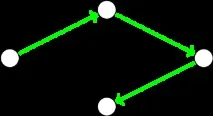
На снимката по-горе минималното обхващащо дърво е избрано и има тегло6, но след добавяне на две дъги с тегло1 това става непостижимо. Какво да правя?

Хитри китайци

Как да се справяме с насочените графи беше казано на света през 1965 г. от двама китайци: Чу Йонгжин и ЛиуЗенхонг. Независимо от тях, приблизително по същото време (публикуван през 1967 г.), подобен алгоритъм е разработен от Джак Едмъндс. Задачата не е много трудна. Също и алчност, просто малко по-трудно, отколкото за неориентиран график.

Като начало нека дефинираме малко задачата. Има вариант, който описах в "Коварни стрели", когато отговорът е гора от вкоренени дървета (това, което се наричаразклоняване, "разклоняване"). И има вариант с избран корен, тогава се изисква да се изгради дърво с минимално тегло, окачено на този корен (съответно,arborescence, „дървовидна формация“). Първият вариант може лесно да се сведе до втория: добавяме фиктивен корен към графиката и начертаваме дъга с безкрайно тегло към всеки връх от този корен. Безкрайността, както обикновено, трябва да бъде избрана внимателно, така че да може да се извади нещо от нея и след това дори да се сравни.

Редукцията в обратната посока е още по-проста: изхвърляме дъгите, отиващи към корена (те не са в правилния отговор), след това, акодървовидност съществува, тогава оптималноторазклоняване също е оптималнодървовидност. Предлагам да се реши проблемът сдървовидното, защото тогава ще има по-малко неприятни случаи.

Защо не погледнете всички дъги, включени в него за някакъв връх. Ако добавим (или извадим) някакво число към теглото на тези дъги, тогава проблемът няма да се промени: точно една дъга влиза в този връх в отговора и теглото на отговора ще се промени точно с това число. Извадете от дъгите, влизащи във върха, теглото на най-малката от тях.

Сега поне една дъга с тегло нула идва до върха, а теглата на останалите дъги са неотрицателни. Разбира се, бих искал да добавя тази нулева дъга към отговора. Какво ще се случи, ако извършим тази операция с всеки (с изключение на основния) връх на графа?

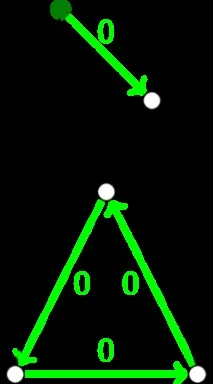
Няма толкова много графи от формата „една дъга идва до всеки връх“. И, нека ви напомня, нулеви дъги влизат в един от върховете: корена на дървото. Могат да се реализират два варианта: скучен и не много. В скучната версия всички върхове ще образуват дърво с нула дъги и това очевидно ще бъде правилният отговор. Но могат да се появят и цикли.

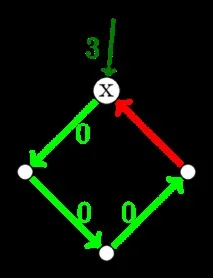
Тук, между другото, е важно, че извадихме теглата на дъгите във върха, а не просто взехме минимума. Значението на цикъла от нулеви дъги е, че можете да стигнете до всеки връх на цикъла и това автоматично ще ни даде пътя до всички останали върхове на цикъла. Тоест, ако стигнем до върхаx, тогава ние просто заместваме нулевата дъга, водеща доx по протежение на цикъла с дъга от външната страна. Ще трябва да платим за тази операция с разликата в теглата на дъгите, следователно, така че при следващата итерация теглото на дъгата да означава цената на добавянето й, ние ще доведем изваденото до нула.

Възстановяване на отговор

Не е много сложно, ако изрично компресирате графиката (и съхранявате кондензации от всяка от компресиите). Необходимо е да се разбере при всеки цикъл коя дъга трябва да бъде изхвърлена. Съвет: този, който идва до върха, посетен от дъгата от най-горното ниво.

Ако компресирате не прости цикли, а компоненти на силна свързаност, тогава ще бъде малко по-трудно да се възстанови. Ще трябва да напишем първо търсене в дълбочина, което, предвид компонента и първия посетен връх, ще даде пътищата до всички останали.

Работни часове

В най-лошия случай може да се окаже, че само един цикъл с дължина две се кондензира на всяка стъпка, след което се достига времето за изпълнение Θ(n m), къдетоn е броят на върховете в графиката, аm е броят на дъгите.

Въпреки това, ако подходите към проблема малко по-внимателно, тогава можете да срещнете O(m log n + n²) или дори O(m log n) (или дори min (m log n, m + n²) , но това ще остане за читателя вкато упражнение).

Тарян можеше да го направи, така че и ние можем да го направим

Имаме нужда от скрап, разглобен газотурбинен двигател и няколко структури от данни. Робърт Тарян написа статията Намиране на оптимални разклонения през 1977 г.

Главна идея

Разбира се, никой не иска изрично да преустройва графиката след всяко компресиране на цикъла. Просто трябва да работите не с върхове, а с техните групи (по-нататък ще ги наричам "компоненти"). Можете да ги съхранявате в най-често срещаната система от несвързани множества. Удобно е да включите в отделен компонент върховете, за които вече е намерен отговор ("нулевия" път от корена), заедно със самия корен.

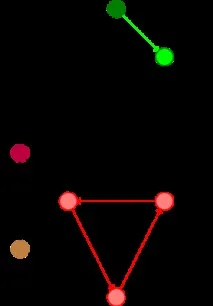
Тогава можете да се възползвате от факта, че основният алгоритъм е алчността. В какъв ред да вземете нулеви дъги - няма значение, коректността не се променя от това, можете да го направите, както е по-удобно. Лично за мен е по-удобно да взема върха и да вървя от него към корена. Тоест намерете минималната входяща дъга, извадете, преминете през нула, вземете минималната дъга, извадете, преминете през и т.н.

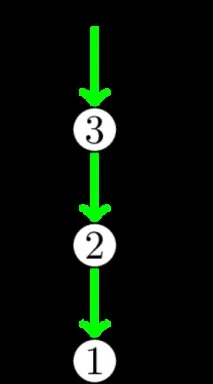
Такова пътуване може да завърши по един от двата начина. Първо: преминавайки по следващата дъга, стигаме до коренния компонент (т.е. до самия корен или до върха, до който вече има път от корена). Това просто означава, че за оригиналния връх (и за всички върхове по пътя) отговорът също е намерен, остава да го възстановим и да обединим компонентите с корена.

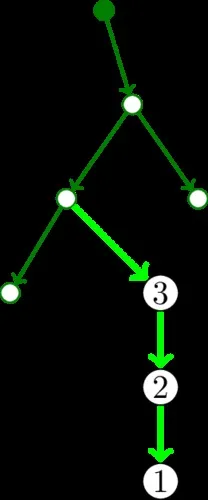
Друг вариант ще разстрои феновете на играта със змии, но ще зарадва древните гърци с буквата ρ. Минавайки по дъгата, ще стигнем до върха на пътеката, която посетихме не толкова отдавна. Здравей цикъл.

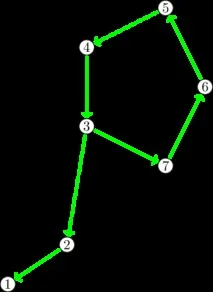
Време е да компресирате този цикъл (т.е. да комбинирате неговите компоненти в едно - не забравяйте, че компресията е изключително имплицитна). Това може да се направи за размера на цикъла (като се премине през него отново), след товазащо да продължим кампанията, но вече обработваме предишния цикъл като един компонент. Компонентът в графиката е станал по-малък, което означава, че рано или късно, компресирайки много, много цикли, ще стигнем до корена.

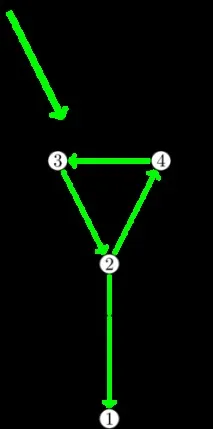
Нека преминем през всички върхове на графа и след като срещнем този, който все още не е обработен, ще го доведем до корена по описания по-горе начин (може би ще обработим не само него, но и още няколко върха по пътя).

Внедряване

Но за такива трикове ви е необходима втора структура от данни: трябва бързо да изберете минималната входяща дъга от цял компонент. Структурата трябва да съхранява набора от входящи дъги (алтернативно, сортирайте входящите дъги за всеки връх предварително и съхранявайте набора от върхове). Искаме следното от структурата на данните:

вземете минимума
премахнете минимума (алтернативно вземете следващата дъга в списъка с върхове и променете една стойност в структурата на данните)
добавете число към всички тегла
обединяване на две структури в една

Операцията „премахване на минимума“ е необходима поради следната причина. „Мързеливото“ компресиране на графиката означава, че никой няма да премахне цикли (дъги вътре в компонента). Следователно операцията "вземете минималната дъга, включена в компонента" може да върне дъгата, излъчвана от същия компонент. В този случай просто трябва да премахнете тази дъга от структурата на данните (всяка дъга на графиката ще трябва да бъде изтрита не повече от веднъж, времето за изпълнение не се влияе) и опитайте да вземете минимума отново.

Има доста опции за структура на данните за такъв случай. Декартово дърво по скрит ключ с произволен приоритет, изчислен минимум на поддървета и операция върху сегмент. Разклонете дърветата с правилния подход. Някои сливат купчини. Или поне чифт std::set и shift: вземете подхода „при конкатенация“елементи от по-малкия и един по един добавете към по-големия ” дава прехвърлянето на всеки елемент не повече от веднъж, но този логаритъм ще излезе отново в асимптотиката на времето на работа: .

Ще оставя и подробен анализ на работното време на читателя, остава един интересен момент.

Възстановяване на отговор

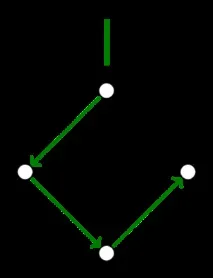
Необходимо е да се разбере кои от дъгите, взети в хода на алгоритъма, трябва да бъдат оставени и кои трябва да бъдат премахнати, за да се отворят циклите. За да направите това, трябва да запомните как сме компресирали графиката, в противен случай информацията няма да е достатъчна. На снимката има две еднакви графики, но ако цикълътb →c →d е бил компресиран първо, тогава дъгатаed трябва да бъде изхвърлена заедно сdb, а ако цикълътb →e →d, тогава дъгатаcd.

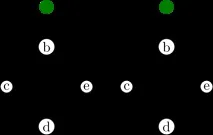
Нещо повече, дъгитеcd иed можеха да имат различни тегла, преди минимумите да бъдат извадени, тъй като бяха зададени на нула на различни стъпки.

Това означава, че за да реконструирате отговора, трябва честно да преминете към компонентите. За всеки (появяващ се в хода на алгоритъма) компонент, запомнете от какви компоненти на по-ниско ниво се състои и ние ще го разширим рекурсивно. Но ако решим коя дъга да вземем, тогава трябва да маркираме като постигнати всички компоненти, които включват тази дъга. Да, може да има много от тях (ако дъгата на външното ниво навлезе във връх с голяма дълбочина), но всеки компонент ще бъде достигнат точно веднъж.

Това може да стане лесно, ако предварително за всеки компонент запазите връзка към външното следващо ниво. След това, след като сте решили да вземете някаква дъга в отговор, просто трябва да се изкачите от един връх до компоненти от по-високо ниво и да ги маркирате като посетени. Препоръчвам да номерирате всички компоненти, които се появяват в хода на работа с цели числа.

Благодаря за вниманието

За тези, които са прочели до края,подарък под формата на моя код по тази тема.