Методи за последователна безусловна оптимизация
Когато се използват бариерни функции, изборът на началната стойност
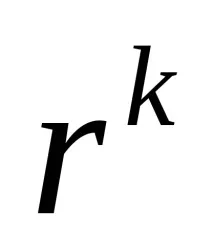
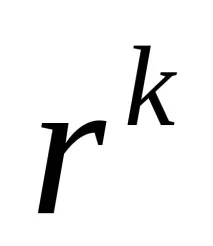
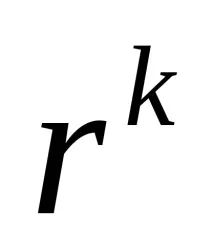
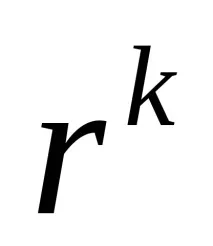
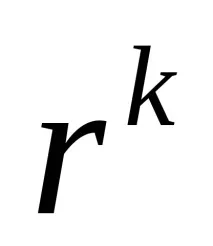
В зависимост от това дали x(k) е допустимо или недопустимо при итерации, методите за условна оптимизация се разделят съответно на вътрешни или външни точкови методи. Ако последователност от x(k) съдържа точки от двата типа, методът се нарича смесен. Методите на вътрешни точки се свързват с такива функции P, за които е известно, че стационарните точки на функцията z са допустими.
Обща моделна схема на последователни безусловни методи за оптимизация
Стъпка 1. Задайте начална точка
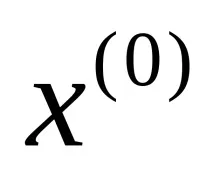
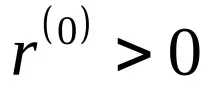
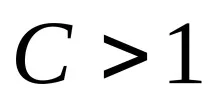
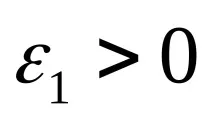
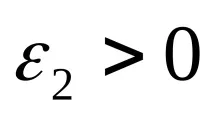
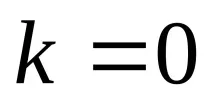
Стъпка 2. Съставете функция
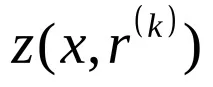
Стъпка 3. Намерете точката
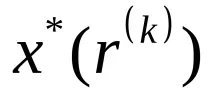
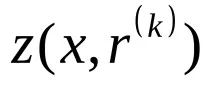
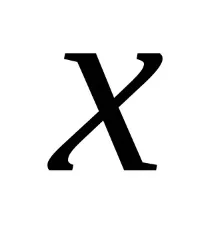
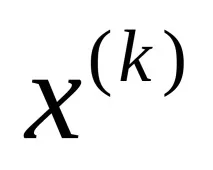
Стъпка 4. Проверете условието за прекратяване:
Ако , процесът на търсене се прекратява
Ако , преизчислете
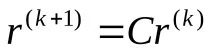
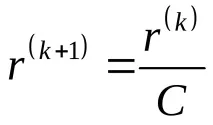
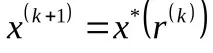
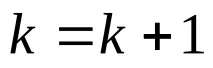
Калкулатор
Услуга за безплатна оценка на цената на работата
- Попълнете заявление. Експертите ще изчислят цената на вашата работа
- Изчисляването на цената ще дойде по пощата и SMS
Номерът на вашето приложение
Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.