Момент на сила спрямо точка и ос - Студиопедия
Да разгледаме тяло с една фиксирана точка O, към която е приложена силав някаква точка A (фиг. 1.9). Тази сила ще се стреми да завърти тялото около точка O. Ротационният ефект зависи от модула на силата, позицията в пространството на равнината, минаваща през точка O и линията на действие на силата, най-късото разстояние от точка O до линията на действие на силата и посоката на силата. Влиянието на всички тези фактори може да се отчете от един вектор, който се нарича момент на силаспрямо точката (центъра) O.
Моментът на сила спрямо някаква точка (център) O е векторът o ( ), приложен в тази точка и насочен перпендикулярно на равнината, минаваща през избраната точка и линията на действие на силата в посоката, от която се вижда силата, стремяща се да завърти тялото около точка O обратно на часовниковата стрелка. Модулът на момента е равен на произведението на модула на силата и най-късото разстояние от точка O до линията на действие на силата, което се нарича рамо на силата спрямо точка O.
С други думи, векторътo( )може да се дефинира като векторен продукт:
o( )=x,(1.2)
къдетоr ерадиус-векторът на точката на прилагане на сила спрямо точката O (фиг. 1.9).
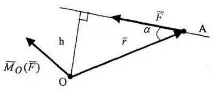
Моментният модул, съгласно правилото за кръстосано произведение, е равен на
= Fr sin= Fh,(1.3)
където е ъгълът между векторитеи;h– рамо на силаспрямо центъра О.
Ако системата се състои от сили, разположени в една и съща равнина (такава система от сили се нарича плоска) и е необходимо да се определят техните моменти спрямо точки от една и съща равнина, тогава няма смисъл да се определят като вектори, тъй като всички те ще бъдат насочени перпендикулярно на равнината на силите. Следователнов случайна плоска система от сили моментът се определя като алгебрична величина:
MO( ) = ±Fh.(1.4)
Освен това моментът на сила спрямо точката се счита за положителен, ако силата се стреми да завърти равнината на чертежа около точката O в посока, обратна на въртенето по посока на часовниковата стрелка, и отрицателна, ако в посоката на въртене по посока на часовниковата стрелка.
Да разгледаме тяло с две неподвижни точкиОиО', към които е приложена силаFв някаква точка А (фиг. 1.10). Тази сила ще се стреми да завърти тялото около оста Oz, минаваща през точките на закрепване. Ротационният ефект зависи от модула на проекцията на силата върху равнина, перпендикулярна на оста Oz; най-късото разстояние от точката на пресичане на оста Oz с равнината до линията на действие на проекцията; посока на проекционния вектор. Всички тези фактори могат да бъдат взети под внимание чрез въвеждане на концепцията за момент на сила около оста.
Моментът на силата F спрямо оста Oz може да се определи като алгебрична величина, равна на момента на проекцията на силата F върху равнината Oxy, перпендикулярна на оста Oz (xy), спрямо точката O на пресичане на тази ос с равнината(фиг. 1.10).
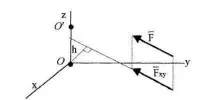
където h е рамото на проекциятаxyспрямо точка O.
Моментът на силата спрямо оста Oz може също да се дефинира като проекцията на момента на силата спрямо произволна точка от оста Oz (например точка O) върху тази ос(фиг. 1.11).
Моментът на сила около остаOzсе счита за положителен, ако, гледайки към положителната посока на оста, може да се види проекцията на силата, стремяща се да завърти равнинатаОхув посока, обратна на въртенето по часовниковата стрелка.
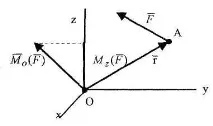
Ако са известни проекциите на силатавърху осите на декартовата координатна система(Fx, Fу, Fz)и координатите на точката на приложение на силата(x, y, z),, тогава моментите на силатаFспрямо осите на тази координатна система може да се определи по формулите:
MX( ) = yFz - zFy; My( )=zFx -xFz; MZ( ) = xFy-yFx.(1.5)
Когато решавате задачи, е много важно да запомните кога моментите на силата спрямо точка и ос са равни на нула.
Моментът на силата около точка е нула, ако линията на действие на силата минава през тази точка, тъй като в този случай рамото на силата е нула.
Силовият момент около оста може да бъде нула в два случая:
а) силата е успоредна на оста, тъй като в този случай проекцията на силата върху равнината , перпендикулярна на дадената ос, е равна на нула;
б) линията на действие на силата пресича оста, тъй като в този случай рамото на проекцията на силата върху равнина, перпендикулярна на дадената ос, спрямо точката на пресичане на оста с равнината е равна на нула.
Ако положението на тялото и посоката на силата са определени в декартовата координатна система, тогава при изчисляване на моментите на сила както спрямо точката (с плоска система от сили), така и спрямо оста, е полезно първо да разложите силите на компоненти, успоредни на координатните оси, да изчислите момента отделно за всеки компонент и след това да ги добавите алгебрично. Според теоремата на Вариньон моментът на резултантните сили спрямо точка (за плоска система от сили) и ос е равен на алгебричната сума на моментите на съставните сили спрямо същата точка или ос.
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо