Мозайка Пенроуз

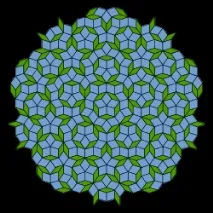
Плочки на Пенроуз,плочки на Пенроузе общото наименование за три типа непериодично разделяне на равнината. Те са кръстени на английския математик Роджър Пенроуз, който изучава тези прегради през 70-те години на ХХ век.

Съдържание

И трите типа подложки на Пенроуз, като всички апериодични подложки, имат следните свойства:

непериодичност - липса на транслационна симетрия,
повторяемост (наричана още самоподобност, която обаче не е свързана с едноименното свойство на фракталите) - всеки произволно голям фрагмент от подредбата на Пенроуз се среща в подложката безкраен брой пъти, макар и през неравни разстояния,
квазикристалност - при дифракция върху мозайка, както върху физическа структура, дифракционната картина показва наличието на далечен ред и симетрия от пети ред.

Периодични и апериодични подреждания

Облицовката е покритие на равнина с плочки без празнини и наслагване на плочки една върху друга. Плочките обикновено могат да приемат краен брой различни форми, наречени протоплочки. Твърди се, че набор от прототили допуска подреждане, ако съществува подреждане на равнината с плочки, които са конгруентни на прототилите на набора.

Подреждането се нарича периодично, ако съществува двупараметърно семейство от паралелни транслации, всяко от които го комбинира със себе си. В противен случай подреждането се нарича непериодично. Най-известните плочки (например плочки с квадрати или триъгълници) са периодични.

Набор от протоплочки се нарича апериодичен, ако допуска подреждане на равнината, но всяко подреждане от тези плочки е непериодично. Облицовката на равнина с плочки от апериодичен набор също се наричаапериодичен.

Ранни апериодични облицовки

През 60-те години на XX век логикът Хао Уанг (англ. Hao wang) разглежда проблема с облицоването на равнината с квадрати с цветни ръбове (сега известни като плочки на Уанг): възможно ли е да се облицова равнината с такива квадрати без завъртания и отражения, така че квадратите да докосват ръбовете от същия цвят.

Уанг отбеляза, че ако този проблем е алгоритмично неразрешим, тогава съществува апериодичен набор от плочки на Уанг. По онова време това се смяташе за малко вероятно, така че Уанг предположи, че проблемът с подреждането е разрешим.

Въпреки това ученикът на Уанг Робърт Бергер показа, че проблемът с подреждането е алгоритмично неразрешим (тоест предположението на Уанг е грешно). Той също така построи комплекта апериодични плочки на Wang от 20 426 плочки. Впоследствие бяха открити апериодични комплекти от по-малко плочки. В момента минимумът е набор от 13 плочки, открити от Карел Чулик през 1996 г.

Въз основа на резултатите на Бергер Рафаел Робинсън получи апериодичен набор, състоящ се само от шест прототила (въртенията и отраженията вече са разрешени).

Разработка на Penrose Mosaics

Първият тип плочка на Пенроуз (P1) също се състои от шест протоплочки, но те не са базирани на квадрат, а на правилен петоъгълник. Въз основа на идеите, изразени от Йоханес Кеплер в Harmonices Mundi, той успява да намери форми на плочки и правила за комбиниране, които гарантират апериодичност на комплекта. Мозайка P1 може да се разглежда като продължение на "фигурата Аа" - крайната фигура, изобразена от Кеплер, съставена от правилни петоъгълници, петолъчни звезди, десетоъгълници и някои други фигури.

Впоследствие Пенроуз успява да намали броя на прототилите до два, получавайкиоще два вида облицовка на Пенроуз: от делтоиди (P2) и от ромби (P3). Ромбовата мозайка на Пенроуз също е открита независимо от Робърт Аман.

През 1981 г. Nicholas de Bruijn описва алгебричен начин за конструиране на подложки на Пенроуз, базиран на пет семейства успоредни прави (или, алтернативно, чрез разрязване на петизмерно пространство с двуизмерна равнина).

Трите вида плочки на Пенроуз имат много общи черти, така че формите на плочките и в трите вида са свързани с правилния петоъгълник и златното сечение. В този случай основните форми трябва да бъдат допълнени с правила за комбиниране, за да се гарантира апериодичност. Правилата за съпоставяне уточняват как съседните плочки могат да се съберат заедно и могат да бъдат приложени чрез маркиране на върхове, ръбове или леко преоформяне (добавяне на подходящи ръбове и вдлъбнатини към ръбовете)

Оригинална облицовка на Penrose (P1)

Този тип облицовка на Пенроуз е изградена от шест вида плочки: три от тях са във формата на правилен петоъгълник (те се различават по правилата за комбиниране), останалите са във формата на петлъчева звезда, „лодка“ (подобна на звезда с два отрязани лъча) и ромб.

Мозайка на Пенроуз от делтоиди (P2)

Вторият тип облицовка на Пенроуз е изградена от два вида плочки: изпъкнал делтоид („змия“) и вдлъбнат делтоид („стреличка“). Тези форми могат да бъдат свързани, за да образуват ромб, но правилата за комбиниране забраняват такава комбинация от плочки в облицовката на Пенроуз.