Образователни елементи (7)

Модул към темата: "Приближени формули в схемата на Бернули"

Цел:Работейки с този модул, ще се запознаете с формулата на Поасон, интегралната и локалната теорема на Моавр-Лаплас, ще научите как да изчислявате вероятността с помощта на тази формула.

Приблизителни формули в схемата на Бернули.

Директното прилагане на формулата на Бернули за голям брой тестове е свързано с тромави изчисления. Следователно, за големи

, вместо него, като правило, се използват приблизителни формули на Поасон и Моавр-Лаплас.

Ако броят на опитите

е достатъчно голям и вероятносттае достатъчно малка и техният продуктне е малък и не е голям (обикновено условията са достатъчни), тогава вероятносттаможе да бъде приблизително намерена с помощта на формулата на Поасон:

Локална теорема на Moivre-Laplace

Ако броят на опитите

е достатъчно голям и вероятноститеине са много близки до нула (обикновено условията са достатъчни), тогава вероятносттаможе да бъде приблизително намерена с помощта на формулата на Moivre-Laplace:

,

където

е функцията на Гаус.

Интегрална теорема на De Moivre-Laplace

При условията на локалната формула на Moivre-Laplace, вероятността броят на успехите

да е междуиможе да бъде приблизително намерена чрез интегралната формула на Moivre-Laplace

,

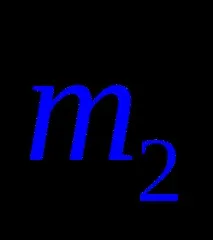
където е функцията на Лаплас

Стойностите на функциите на Гаус и Лаплас се намират в таблиците

Според задачата. Тъй като

е достатъчно голямо,е достатъчно малко, можете да използвате формулата на Поасон, за да изчислите. Имаме , откъдето

Вероятността отделен продукт да бъде дефектен при автоматично щамповане на продукти е постоянна и равна на

. Каква е вероятността в партида от 1000 артикула точно 40ще се жени ли?

Според задачата. Теоретично можете да използвате формулата на Бернули. Полученият израз обаче ще бъде твърде тромав, така че е по-удобно да се приложи локалната формула на Moivre-Laplace. . От тогава .

(стойността на функцията се намира от таблицата). следователно

Вероятността за попадение в целта с бързострелка с един изстрел е 0,75. намерете вероятността при 300 изстрела броят на попаденията да бъде поне 210, но не повече от 230?

Според задачата. За да намерим вероятността, използваме интегралната формула на Moivre-Laplace.

, , Тогава

Прочетете внимателно условията на проблема и изберете желаната формула (Бернули, Поасон или Моавр-Лаплас)

Производителят изпрати 12 000 висококачествени продукта в базата. Броят на продуктите, повредени по време на транспортиране, е средно

. Намерете вероятността базата да получи: а) не повече от три повредени продукта; б) поне две са повредени.

Вероятността за възникване на събитие А във всеки от 900-те независими опита е

. Намерете вероятността събитие А да се случи: а) 750 пъти; б) 710 пъти.

Кълняемостта на семената на това растение е 0,9. Намерете вероятността от 900 засадени семена броят на покълналите семена да е между 790 и 830.

Мишената се състои от три по двойки непресичащи се зони. С един изстрел в мишената вероятността за попадение в първата зона за даден стрелец е 0,5. За втората и третата зона тази вероятност е съответно 0,3 и 0,2. Стрелецът стреля 6 изстрела по целта. Намерете вероятността в този случай да има 3 попадения в първата зона, 2 попадения във втората и 1 попадение в третата зона.

Вероятността за повреда на един елемент от устройството, по време на t часа работа, е равна на0,002. Каква е вероятността за време t от 1500 независимо работещи елемента да откажат: а) 4 елемента; б) не повече от два елемента?

Колко пъти с вероятност от 0,0484 можем да очакваме появата на събитие А в 100 независими опита, ако вероятността за появата му в отделен опит е 0,5.

Вероятността за възникване на събитие А във всеки от 900-те независими опита е

. Намерете вероятността събитие А да се случи поне 710 пъти и най-много 740 пъти.

Двама равни шахматисти играят шах. Какво е по-вероятно: а) да спечелите една игра от две или две от четири игри; б) да спечелите поне два мача от четири или поне три мача от пет? Равенствата не се зачитат.

Вероятността да направите грешка при въвеждане на текст, състоящ се от 1200 знака, е 0,005. Намерете вероятността при въвеждане да бъдат допуснати: а) 6 грешки; б) поне една грешка.

В град N на всеки 100 семейства 85 имат цветни телевизори. Каква е вероятността от 400 семейства 340 да имат еднакви телевизори.

Каква е вероятността от 2450 улични лампи до края на годината да светят между 1500 и 1600? Да приемем, че всяка лампа ще гори една година с вероятност 0,64.

В семейството има 6 деца. Намерете вероятността даденото семейство да има поне две момчета, но не повече от четири. Приемете вероятността да имате момче и момиче като 0,5.

Запишете в бележника си необходимата информация по тази тема.

Запишете решението на задачите в тетрадката си!

Решете проблемите сами, изпратете ги за проверка

По-трудни задачи

Колко произволни числа трябва да се вземат, така че сред тях с вероятност най-малко 0,95 числото 2 да се появи поне веднъж.

X е броят на електроните,излъчени от нагрятия катод на електронната тръба за времето t ,

средният брой излъчени електрони за единица време. Определете вероятността за времетоброят на излъчените електрони да бъде по-малък от.

Застрахователната компания е застраховала 10 000 коли. Вероятността всяка кола да се повреди в резултат на катастрофа е 0,006. всеки собственик на застрахования автомобил плаща 12 рубли на година. застрахователна компания и в случай на повреда на автомобила в резултат на злополука, получава от компанията 1000 рубли Намерете вероятността след една година работа застрахователната компания да претърпи загуба.

При условията на предишната задача намерете вероятността застрахователната компания да реализира печалба от най-малко

рубли.

---