Оценка за консистенция и нейните свойства
Индекс на консистенция и неговите свойства - раздел Обучение, Статистически хипотези в проблемите на обработката на експериментални данни чрез Индекс на консистенция или статистически.
Индикаторът за последователност илистатистическата характеристика на хипотезата е случайна променлива, която е функция на хипотетични данни и резултати от наблюдение, предназначени да тестват нулевата хипотеза.
Конкретната форма на индикатора за съгласуваност за различните хипотези може да бъде различна. Така че, когато тествате хипотеза за закона за разпределение, индикаторът за последователност може да бъде зададен по следните начини:
- като функция на хипотетичната функция на разпределение, т.е. функцията на разпределение, представена като нулева хипотеза, и статистическата функция на разпределение, получена експериментално:
; (6.3.1)
- като зависимост от хипотетичната вероятностpи честотатаp* получени в резултат на експеримента:
.
При тестване на хипотезата за равенството на математическите очаквания на две независими случайни променливи и индикаторът за съгласуваност може да бъде избран под формата на различни видове зависимости от началните и централните моменти на първия и втория ред на случайни променливи и :
.
Прилагат се и други типове зависимости. Но въпреки това разнообразие, във всеки случай индикаторът за последователност трябва да отговаря на редица изисквания. Тъй като тази стойност е случайна, изискванията са формулирани и във връзка със закона за разпределение на индекса на консистенция. Те се състоят в следното.
1. Показателят за последователност трябва да се определя от нулевите и конкуриращите се хипотези, както и от условията на експеримента. Така че, по отношение на последователността,дефинирана от израз (6.3.1), тази зависимост е представена от наличието както на хипотетични, така и на статистически функции на разпределение като аргументи на функциятаf1.
2. Индикаторът за съгласуваност трябва да бъде случайна величина, чието точно или приблизително разпределение е известно. В момента най-често срещаният избор на показатели за последователност, разпределени според нормалния закон, законите на хи-квадрат, Студент, Фишер. Освен това показателите за съответствие с различни закони на разпределение се обозначават с различни символи. И така, показателите, разпределени според нормалния закон, се означават сuилиz, според закона хи-квадрат - чрез c 2, според закона на Стюдънт - чрезt, според закона на Фишер - чрез F.
3. Законът за разпределение на индикатора за съгласуваност трябва да бъде инвариантен спрямо формата на закона за разпределение на изследваната случайна величина. Именно това обстоятелство определи широкото разпространение на показателите за последователност, които имат посочените по-горе закони за разпределение.
4. За да се изгради законът за разпределение на индикатора за консистенция, трябва да се изисква минимум априорна информация, тъй като възможността за получаване на надеждна информация преди експеримента е значително ограничена.
5. Законът за разпределение на индикатора за последователност трябва да бъде критичен по отношение на тестваната хипотеза. Това изискване означава, че условните плътности на разпределение и трябва да се различават значително една от друга.
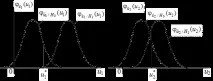
Фиг.6.1. Условни плътности на разпределение на индикаторите за консистенция
Фигура 6.1 показва кривите на условната плътност на разпределение на два различни индикатора за съгласуваност както при нулевата, така и при конкурентната хипотеза. Сравнението на кривите показва, че използването на индикатора е за предпочитане,тъй като осигурява по-висока степен на увереност при разграничаване на хипотезитеH0 иH1 от индекса. Наистина, за същата стойност на , т.е. когато се случи същото събитие, вероятността то да се отнесе към нулевата хипотеза е много по-висока, когато се използва индикаторът.
В заключение трябва да се отбележи, че за да се тества хипотезата, частичните стойности на стойностите, включени в индикатора за съгласуваност, се изчисляват от примерните данни и по този начин се получава частичната стойност на индикатора за съгласуваност на хипотезата. Тази стойност, изчислена от примерните данни, ще се наричанаблюдавана стойност на индекса на консистенция и ще се обозначава сu.