Ограничения на безконтекстната граматика, платформа за съдържание

10. Ограничения на безконтекстната граматика
Доказателство. Вземете граматика в нормална форма на Чомски, която разпознава езикаL. НекаNе множеството от неговите нетерминали. Означавамеn=N. Ние взимаме:
Некаa:ОLиa>k. Тогаваa>2n-1. Дървото за разбор за изходаaе двоично и само при най-ниските преходи от нетерминал към терминал има един клон. Ако височината на едно дърво е броят на ръбовете в най-дългия му клон, тогава е съвсем очевидно, че това е същото като броя на нетерминалитенанеговия най-дълъг клон. Ако височината е строго по-голяма отn, тогава някои не-терминали на клона неизбежно ще се повторят. Ако височината е ограничена от числотоn, тогава по протежение на всяко разклонение бифуркацията възниква във всички некрайни върхове, с изключение нанай-ниските, напредпоследнитенива.
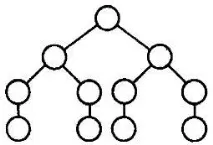
Дължината на последната дума в такова дърво не може да надвишава2n-1. Следователно, в максималния клон на дървото за анализ за нашияa, някои нетерминалниAще се появят повече от веднъж. Следващата фигура ясно илюстрира какво еu,x,v,y,w.
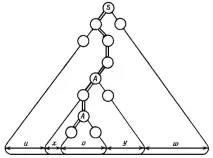
Ако обърнем внимание на доказателството на тази теорема, можем да извлечем следния факт.
Лема.НекаL–свободен от контекста и безкраен език,k –число оттеорема за изпомпване. Тогава вLима поне една думаaдължинаот коятосе подчинява на условието:k2k, след товаuw>k. Особеноuvw>k. Но думатаuvwсе намира вLи е по-кратка отa, което противоречи на нашия избор наa. Така чеa£2k, както се изисква.
Следствие от тази лема е основният резултат
Теорема.Проблемът за ограничеността на езика за класа от контекстно-свободни граматики е алгоритмично разрешим.
Теоремата означава, че има алгоритъм, който, като се има предвид всяка безконтекстна граматика, определя в краен брой стъпки дали езикът, генериран от тази граматика, е безкраен или не. Алгоритъмът е следният. При дадена граматикаG, ние конструираме еквивалентна граматикаG’в нормална форма на Чомски. Некаnе броят на нетерминалите вG’. Чрез изброяване на всички възможни изводи вG’, можем да определим дали граматиката, генерирана отG’(и, следователно, генерирана отG) има поне една дума, чиято дължина е по-голяма от2n, но не по-голяма от2n+1. По лемата това ще бъде критерият за безкрайност на езика.
Ако „разровим“ малко по-дълбоко в доказателството на теоремата за изпомпване, можем да извлечем такъв факт.
Лемата означава, че за да се провери безкрайността на KS-lime, е достатъчно след привеждане на граматиката му в нормалната форма на Khomsky да се проверят само много думи с дължини, по-големи от2n-12n2 8> , което е малко по-добро от предишния алгоритъм.
11.Нормална форма на Грайбах
Ние казваме без контекстграматикаGиманормална форма на Грайбах, ако всяко нейно правило има един от следните четири типа:
къдетоA, B, Cса нетерминали,aе терминал.
Теорема.Всяка граматика без контекст е еквивалентна на някаква граматика в нормална форма на Грайбах.
Идея на доказателството.Разгледайте случая, когато граматиката не съдържа празна дума. Първо, намерете граматика, еквивалентна наGи в нормална форма на Чомски. НекаPса неговите продукти. Тогава правилата в нормалната форма на Чомски имат една от следните форми:A®a,A®BC,иBиCне съвпадат с началния нетерминалS.
Разгледайте в граматикатаGсамо правилатаA®BCи всички изреченски форми, получени от тези правила. Нека обозначим набора от тези правила катоP
Имаме изявление
Този оператор дефинира определен набор от низовеb, за които ще въведем нотация под формата на нов нетерминален символ:XAB
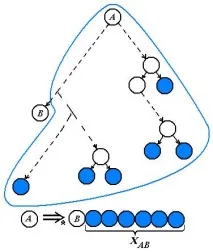
Фигурата показва дървото за двоичен анализ за извеждане на низаBb.Синята линия очертава областта, свързана сb.
Нека добавим нови нетерминали към нетерминалиG(по един нов символ за всяка подредена двойкаA,B) и се опитаме да разширим правилата по този начинP
така че реално да реализират посочения смисъл. На първо място добавяме
Нека сега разгледаме по-подробно дървото за разбор на изразаAÞ*Bbза непразнотоb.
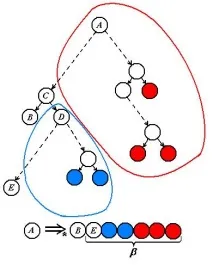
В това двоично дървопоявата на букватаBсе появява в края на най-левия клон чрез прилагане на някое правилоC®BD. Думатаbсе извежда частично отDи частично отA,което е в червената област. Фигурата ясно показва, че тези части отговарят на концепциитеXDEиXAC. Необходимо е само да добавите още една букваEпредXDE. Следователно правилото е:
Тези правила трябва да се добавят към граматиката за всекиC®BDотP
и всяка двойка стари нетерминалиA,E. По-специално правилото ще бъде добавено
от което, като се имат предвид правилата (1), следваXСBÞ*D.
След добавяне къмP
от всички тези правила (1) и (2) ще направим решителна стъпка - ще изхвърлим всички стари правила. Ще останат само нови, чийто набор ще бъде означен сP^.
АкоAÞ*Bb, тогава процедираме както при прехода от фигура към фигура получаваме
Накратко, чрез математическа индукция върху дължината на думатаbот нетерминалите на граматикатаGе необходимо да се покаже:
Освен това граматикатаP^е завършена както следва. Ако правилатаPна първоначалната граматикаGсъдържат производствотоA®a, тогава вP^добавяме
Производството е съвсем естествено - ако вP
И накрая, нека направим последната промяна. Заменяме всяка продукция от тип (2) с няколко продукции
върху всички такива терминалиe, за коитоPсъдържа правилотоE®e.Ако няма такова правило вP, тогава производството (2) е простоизхвърлям. Получената граматика ще бъде желаната.
12. Редовни граматики
Спомнете си, че при компилирането на почти всеки език на високо ниво началните и основните етапи са лексикален и синтактичен анализ. Основната част от анализа е изграждането на дървото за разбор. Това дърво е доста подобно на дървото за разбор за верижно свързване в COP граматика. Ролята на граматика за език за програмиране се играе от описанието на този език под формата на нормална форма на Backus-Naur. Веригата, за която са изградени изходът и дървото за разбор, е програмата, която се компилира.
Въпреки това, предварителният етап е лексикален анализ, който позволява, просто казано, да преименувате някои фрагменти от програмния текст, давайки им статус на терминални символи. Оказва се, че на този етап също е възможно да се използва математическият апарат на COP-граматиките, но в най-простата му форма - под формата на регулярни граматики.
Спомнете си, че CFG се наричаобикновен, ако всичките му правила имат една от следните форми:A®e,A®a,A®aB.
Един езикLсе казва, че еправилен, ако е дефиниран от някаква правилна граматика.
Правилата от форматаA®e, както в граматиките без контекст, не играят съществена роля. Алгоритъмът за премахване наe-правилата оставя правилната граматика правилна. Следователно твърденията заe-свободни регулярни граматики са всъщност твърдения за всички регулярни граматики.
Пример.ГраматикаS®pA,A®iiSдефинира набор от думи във форматаpipipi... За илюстрация разгледайте дървото за разбор на изречениетоpipiвдадена редовна граматика.
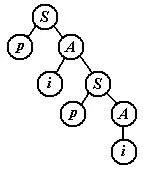
Всяко дърво за разбор в обикновена граматика има същата форма. Въпреки привидната си простота, обикновените граматики все пак имат изразителната сила, достатъчна за изпълнение на задачите на лексикалния анализ. Ограниченията на неговите възможности демонстрират
Теорема (за изпомпване на нормален език).НекаL-произволен нормален иe-свободен език. Некаnе броят на нетерминалите в някаква регулярна иe-свободна граматика, дефиниращаL. Тогава за всяка думаaОLс дължинаa>n:
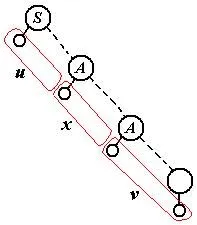
Очевидно броят на нетерминалите в дървото е дължината на изходната верига. Така че някои нетерминални се срещат два пъти. Помислете за „най-горната“ двойка от такива нетерминалиA, в смисъл, че няма повтарящи се нетерминали над долнатаAна тази двойка. Фигурата илюстрира какво еu,x,v. Ясно е, че заедно сaотSсе извеждат всички думи от форматаuxiv(i= 0,1,2,…)букви, дължината на тази последователност и заедно с нея думатаuxне превишаваn. Теоремата е доказана.
Виждаме, че обикновените граматики са по-слаби от тези без контекст. Въпреки това, тяхната изразителна сила е достатъчна за лексикален анализ. Нека дадем няколко примера, илюстриращи тези възможности.
Тази граматика очевидно дефинира езика на целочислените числови константи. Тя не изглежда редовна. Въпреки това веригатаправилоS® може да бъде „елиминирано“ нетерминалното в първото и други правила могат да бъдат заменени с две опции „+ –“, по подобен начин в третото и другите правила заменете нетерминалното със съответните терминали. Резултатът е еквивалентна редовна граматика.
Тази граматика дефинира нормален език на идентификаторите.