Периметри на фигури
Правоъгълник е четириъгълник с четири прави ъгъла. Размерите на правоъгълника са зададени
дължините на неговите страни, обикновено означавани с a и b. Правоъгълник с равни страни (a = b)
Периметърът на правоъгълника ABCD е равен на сумата
страни, умножени по 2 в съседство с един ъгъл.
където P е периметърът на правоъгълника,
a - дължина на първата страна,
b е дължината на втората страна.
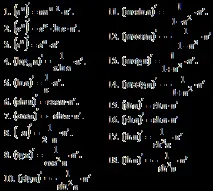
Как да намерите периметъра на правоъгълник по други начини? По-долу са дадени формулите за
намерете периметъра на правоъгълника чрез различни данни.
Формулата за периметъра на правоъгълник по отношение на двете страни на правоъгълника е:
Формулата за периметъра на правоъгълник по отношение на площта и всяка страна:
Формулата за периметъра на правоъгълник по отношение на диагонала и всяка страна е:
Формулата за периметъра на правоъгълник по отношение на радиуса на описаната окръжност и всяка страна:
Формулата за периметъра на правоъгълник по отношение на диаметъра на описаната окръжност и всяка страна:
Основни свойства на правоъгълник.
- Противоположните страни на правоъгълник са с еднаква дължина, тоест те са равни:
- Противоположните страни на правоъгълник са успоредни:
- Съседните страни на правоъгълник винаги са перпендикулярни:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
- И четирите ъгъла на правоъгълника са прави ъгли:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
- Сумата от ъглите на правоъгълник е 360 градуса:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
- Диагоналите на правоъгълник имат еднаква дължина:
- Сборът от квадратите на диагонала на правоъгълник е равен на сбора от квадратитестрани:
2d2 = 2a2 + 2b2
- Всеки диагонал на правоъгълник разделя правоъгълника на две еднакви фигури, а именно
- Диагоналите на правоъгълника се пресичат и разполовяват в точката на пресичане:
AO = BO = CO = DO = d/2
- Пресечната точка на диагоналите се нарича център на правоъгълника и също е център
- Диагоналът на правоъгълника е диаметърът на описаната окръжност.
- Окръжност винаги може да бъде описана около правоъгълник, тъй като сборът от противоположни ъгли
е равно на 180 градуса:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
- Правоъгълник, чиято дължина не е равна на ширината му, не може да бъде вписан с окръжност, тъй като сумите
противоположните страни не са равни една на друга (можете да впишете кръг само в специалния случай